Владимир Живетин - Технический риск (элементы анализа по этапам жизненного цикла ЛА)

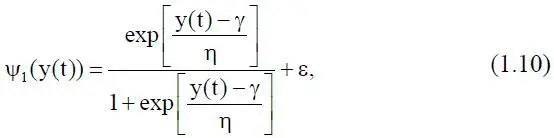
если плотность ω(z) представима в виде плотности S B-распределения Джонсона;

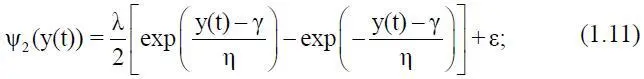
если плотность ω(z) пред ставима в виде плотности S U-распределения Джонсона;

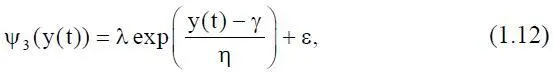
если плотность ω(z) представима в виде плотности S L-распределения Джонсона.

Входящие в выражения (1.10)÷(1.12) параметры λ, γ, η и ε являются параметрами, соответствующими S-распределению Джонсона. Таким образом,

z(t) = ψ j(y(t)), (113)

где 1 ≤ j ≤ 3 в зависимости от вида плотности S-распределения Джонсона, аппроксимирующей заданную плотность ω(z).

Для того, чтобы случайный процесс z(t) имел заданную корреляционную функцию B z(τ), необходимо подобрать соответствующую функцию (обозначим ее ρ y(τ)) нормированному гауссовскому процессу y(t), подвергаемому нелинейному преобразованию ψ j(·) (1 ≤ j ≤ 3). Поэтому на втором этапе проводится расчет корреляционной функции ρ y(r), который осуществляется по формуле

где

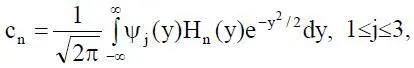
Н n – полином Эрмита n-й степени. Расчет заключается в получении набора значений ρ y(τ i) 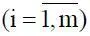корреляционной функции случайного процесса y(t), соответствующих выбранным значениям τ iее аргумента и удовлетворяющих (1.14). При проведении конкретных расчетов ряд, стоящий в правой части этого равенства, необходимо ограничить несколькими первыми членами; количество оставленных членов должно быть таким, чтобы обеспечивалась требуемая точность выдерживания указанного равенства.

На третьем этапе осуществляется представление случайного процесса y(t) в виде компонент двумерного линейного марковского процесса. При этом полученные на предыдущем этапе значения корреляционной функции ρ y(τ) процесса y(t) сглаживаются выражением

ρ y(τ) = e –h|τ|(cosωτ + βsinω|τ|). (115)

Обеспечение хорошей точности сглаживания позволяет, используя приведенную в [6, 18, 44, 47, 71, 74, 75] методику, представить случайный процесс y(t) в виде линейного двумерного марковского процесса (y 1(t), y 2(t)), порождаемого следующей системой стохастических дифференциальных уравнений:

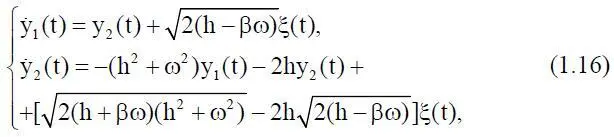
где ξ(t) – гауссовский белый шум с нулевым математическим ожиданием и дельтаобразной корреляционный функцией.

Отметим, что часто встречающиеся на практике корреляционные функции вида

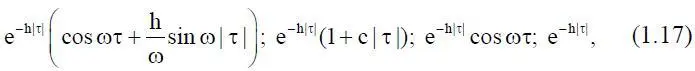
представляют собой частные случаи корреляционной функции (1.15), следовательно, процесс y(t), корреляционная функция которого принадлежит семейству (1.17), может быть представлен в виде компоненты y 1(t) марковского процесса (1.16) после его соответствующего упрощения.

Таким образом, генерация стационарного процесса z(t) с заданными одномерной плоскостью распределения ω(z) и корреляционной функцией B z(τ) может быть осуществлена путем генерации двумерного линейного марковского процесса (y 1(t), y 2(t)), описываемого системой уравнений (1.15), и последующего преобразования с помощью соотношения (1.13) компоненты y 1(t) данного процесса, которое необходимо проводить после установления ее стационарности. При этом двумерный марковский процесс (y 1(t), y 2(t)) может быть получен, например, как выходной процесс с формирующего фильтра [69], возбуждаемого белым шумом с указанными статистическими характеристиками и построенного в соответствии с системой (1.16).

Оправдывает ли себя в эксплуатации тот или иной ЛА, окупятся ли расходы разработки, изготовления и эксплуатации тех или иных новых систем бортового оборудования или новых конструкций планера и двигателя? Технологии их изготовления (рис. 1.19) зависят от соотношения прибыли и потерь при эксплуатации, характеризуемые вероятностями P 1и P = (P 2, P 3, P 4). При анализе P 1и P необходимо учитывать целевое назначение ЛА в силу различия, например, спортивных самолетов от самолетов гражданской авиации, для которых, в отличие от первых решающее значение имеет место выход параметров траектории полета в критическую область.

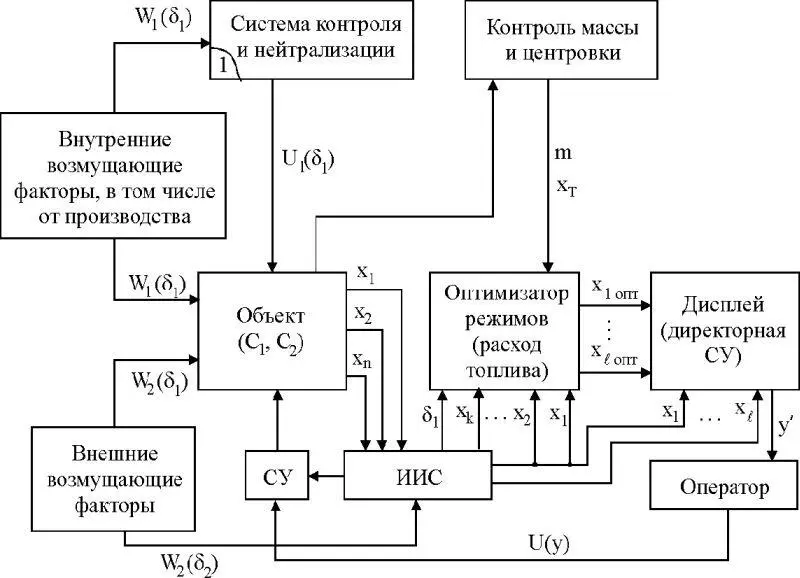
Рис. 1.19. (Здесь 1 – система встроенного контроля бортового оборудования; y = (x 1 опт, …, х l опт, х 1, …, х ι, δ 11, …, δ 1α), W 2(δ 2) – внешние возмущающие факторы, в том числе от аэродромных средств посадки, управления воздушным движением, состояния атмосферы, СУ – система управления, ИИС – информационно-измерительная система)

Согласно сказанному выше, имеет место несколько групп параметров траектории полета, которые при эксплуатации ЛА подлежат контролю и управлению. Одна из групп А принадлежит области G 1оптимальных значений. Как правило, G 1узкая, а параметры, принадлежащие G 1, должны измеряться и выдерживаться с высокой точностью. Вторая группа B должна принадлежать области G 2(достаточно большой) допустимых значений. Выход параметров B из области G 2связан с потерями техники, в том числе с ее восстановлением.

Параметры, принадлежащие A и B при эксплуатации ЛА, подлежат контролю и управлению. Кроме управляющих воздействий они изменяются под действием возмущающих факторов внутреннего и внешнего происхождения, которые обуславливают их выход из G 1и G 2и соответствующие потери. Как правило, указанные факторы не поддаются контролю или неконтролируемы по каким-либо причинам. Как только тот или иной возмущающий фактор начинают контролировать с помощью бортового оборудования, он переходит в разряд параметров состояния ЛА. Среди таких параметров можно рассматривать массу m и центровку x TЛА.

Некоторые возмущающие факторы, например, параметры восходящих потоков, сдвиг ветра, мы можем только контролировать. Среди внутренних возмущающих факторов выделим следующие (рис. 1.19):

1) технологические факторы производства планера и двигателя, которые обуславливают некоторые колебания аэродинамических характеристик планера на величину ΔY, ΔX, ΔM, где Y, X, M – подъемная сила, сопротивление и момент ЛА соответственно, а также колебания газодинамических характеристик двигателя на величину ΔP, где P – тяга двигателя, которые обозначим C 1, C 2, C 3, C 4соответственно;