Фрэнк Фабоцци - Рынок облигаций. Анализ и стратегии

Цена любого финансового инструмента равна приведенной стоимости предполагаемого денежного потока от данного финансового инструмента. Таким образом, для определения цены следует знать:

1) размер предполагаемых денежных потоков;

2) величину подходящей требуемой доходности (требуемой ставки).

Предполагаемые денежные потоки для одних финансовых инструментов вычисляются легко, для других – с большей сложностью. Требуемая доходность – это величина, отражающая доходность финансовых инструментов со сравнимымриском, иными словами – доходность альтернативных инвестиций.

Первый шаг, который мы делаем, приступая к определению цены облигации, – определение ее денежных потоков. Денежные потоки от облигации, которую эмитент не имеет права погасить до установленной даты погашения (т. е. облигация без встроенного колл-опциона) [7] Ценообразование облигаций со встроенными колл-опционами описано в главе 17. , состоят из:

1) периодических купонных выплат, осуществляемых вплоть до даты погашения;

2) номинальной стоимости (стоимости погашения), получаемой в момент погашения облигации.

Для упрощения анализа механизма ценообразования облигаций, договоримся считать действительными три утверждения:

1. Купонные выплаты осуществляются раз в полгода (по большинству американских облигаций купон действительно выплачивается раз в шесть месяцев).

2. Ближайшая выплата купона состоится ровно через шесть месяцев.

3. Купонная ставка фиксирована на весь срок до погашения облигации.

Итак, денежный поток облигации без встроенного колл-опциона состоит из аннуитета фиксированных купонных выплат, получаемых раз в полгода, и номинальной стоимости. 20-летняя облигация с купонной ставкой 10 % и номиналом $1000 от купонных выплат получит следующий денежный поток:

Таким образом, существует 40 денежных потоков по $50, получаемых каждые полгода, и денежный поток, равный $1000, который будет получен через 40 полугодовых периодов. Обратите внимание на описание номинальной стоимости. Мы не говорим, что получим ее через 20 лет – номинал описывается в тех же терминах, что и купон, выплачиваемый раз в шесть месяцев.

Требуемая доходность выясняется после изучения рыночных доходностей облигаций, сравнимых с нашей. Под сравнимыми понимаются облигации без встроенного колл-опциона, имеющие то же кредитное качество и тот же срок до погашения [8] В главе 4 вводится мера риска процентных ставок, известная как дюрация. Таким образом, сравнимыми мы будем в дальнейшем называть облигации с одинаковой дюрацией, а не сроком до погашения. .

Требуемая доходность, как правило, выражается в процентах годовых. В ситуации, когда денежные потоки поступают раз в полгода, в качестве процентной ставки для дисконтирования денежных потоков принято использовать половину годовой процентной ставки.

Размеры денежных потоков и требуемая доходность – аналитические данные, достаточные для вычисления цены облигации. Поскольку ценой облигации является приведенная стоимость денежных потоков, ее значение вычисляется путем сложения следующих двух величин:

1) приведенной стоимости полугодовых купонных выплат;

2) приведенной стоимости номинала в момент погашения.

В общих чертах формула подсчета цены выглядит следующим образом:

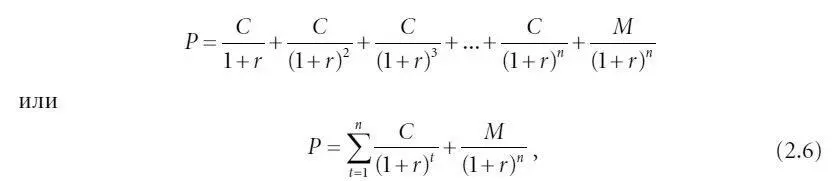
где:

P – цена (в долларах);

n – число периодов до погашения (число лет, умноженное на 2);

C – полугодовая купонная выплата (в долларах);

r – процентная ставка, соответствующая периоду (требуемая годовая доходность, деленная на 2);

M – стоимость номинала;

t – количество периодов, оставшихся до получения платежа.

Полугодовые выплаты купона представляют собой обычный аннуитет, поэтому, используя формулу (2.5) для вычисления приведенной стоимости обычного аннуитета, получаем приведенную стоимость купонной выплаты, равную:

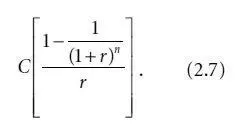
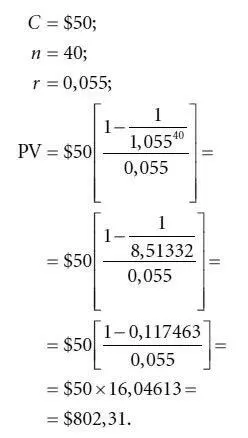
Для того чтобы читатель понял, как на практике осуществляется вычисление цены облигации, рассмотрим 20-летнюю облигацию с купоном, равным 10 %, и номинальной стоимостью $1000. Допустим, что требуемая доходность для этой облигации составляет 11 %. Данная облигация приносит следующие денежные потоки:

1) 40 полугодовых купонных выплат по $50 каждая;

2) $1000 через 40 полугодовых периодов.

Полугодовая (соответствующая периоду) процентная ставка (или соответствующая периоду требуемая доходность) равна 5,5 % (11 % поделить на 2).

Приведенная стоимость 40 полугодовых купонных выплат по $50, дисконтированная по 5,5 %, согласно результатам приведенных ниже вычислений, составляет $802,31:

Приведенная стоимость номинала в $1000, который будет получен через 40 полугодовых периодов , дисконтированная по 5,5 %, равна, как видно из расчетов, приведенных ниже, $117,46:

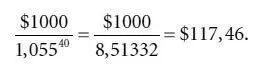
Цена облигации, таким образом, равна сумме двух приведенных стоимостей:

Предположим теперь, что требуемая доходность составляет не 11 %, а 6,8 %. Цена облигации в этом случае окажется равной $1347,04 (процесс вычисления значения цены описан ниже).

Приведенная стоимость купонных выплат при соответствующей периоду процентной ставке 3,4 % (6,8 % /2) равна:

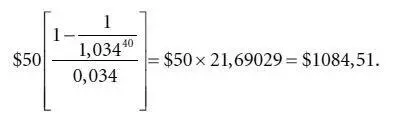
Приведенная стоимость номинала в $1000, который будет получен через 40 полугодовых периодов , дисконтированная по 3,4 %, равна:

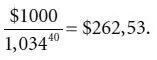
Цена облигации, таким образом, составит:

Если требуемая доходность равна купонной ставке 10 %, цена облигации будет равна ее номинальной стоимости, т. е. $1000. Действительно, приведенная стоимость купонных выплат при соответствующей периоду процентной ставке 5 % (10 %/2) равна: