Джон Грин - Многочисленные Катерины

Когда они проехали мимо магазина, Гассан сказал:

– Не обязательно ехать в «Хардис». Можем поехать куда угодно.

– Здорово. Я, честно говоря, совсем не хочу в «Хардис», – сказала Линдси. – Кормят там так себе. В двух поворотах отсюда, в Милане, есть «Вендис», там намного лучше. У них хотя бы салаты есть.

Поэтому Колин проехал мимо «Хардис» и выехал на шоссе, ведущее на север. Мимо него, одна за другой, мчались машины, а он думал о промежутке между тем, что мы помним, и тем, что случилось, между нашими предсказаниями и тем, что случится. В этом промежутке, подумал Колин, есть место для преображения – он мог перестать быть вундеркиндом и придумать себе новую интересную историю, перерождаться снова и снова. Например, он мог стать змееборцем, эрцгерцогом, победителем ДК – и даже гением. Кем угодно – только не тем, кем уже был раньше. Из путешествия в Гатшот Колин извлек один урок – будущее нельзя предотвратить. И впервые в жизни он улыбнулся, думая о вечно приближающемся, бесконечном будущем, которое простиралось перед ним.

Они ехали дальше. Линдси повернулась к Колину и сказала:

– Знаешь, а ведь вовсе не обязательно останавливаться.

Между сиденьями просунулся Гассан:

– Кстати, да. Не будем останавливаться.

Колин нажал на педаль газа, думая о том, как много дорог открыто для них и как не скоро кончится лето. Линдси Ли Уэллс, сидевшая рядом, коснулась его руки и сказала:

– Да. В самом деле. Едем дальше.

И по спине Колина побежали мурашки. Он вдруг ощутил родство со всеми, кто сидел сейчас в его машине. И со всеми, кто в ней не сидел. И понял, что он не уникален, – в самом лучшем смысле этого слова.

Одна из сносок в романе, который вы только что закончили читать, если, конечно, не заглянули в конец (вернись и читай с начала и до конца, не пытайся узнать, чем все закончилось, хитрый плут!), обещала математическое приложение. Вот и оно.

Так уж вышло, что в одиннадцатом классе я получил тройку с минусом по алгебре, несмотря на героические усилия моего учителя математики мистера Лантрипа. А потом я учил что-то под названием «конечная математика», потому что этот курс был намного проще алгебры. После школы я выбрал тот университет, где не нужно было сдавать математику. Но после того, как я его закончил – знаю, это прозвучит странно, – я даже немного заинтересовался математикой. Но, к сожалению, я до сих пор ничего не смыслю в ней. Я интересуюсь математикой так же, как в девять лет интересовался скейтбордом. Я много о ней говорю и много о ней думаю, но на самом деле совсем ей не занимаюсь.

К счастью, я дружу с парнем по имени Дэниэл Бисс, одним из лучших молодых математиков Америки. Дэниэл – математик с мировым именем, которое он заслужил благодаря опубликованной несколько лет назад научной работе, в которой, судя по всему, доказал, что окружности – это жирные, раздутые треугольники. А еще он – один из моих самых лучших друзей. Именно благодаря Дэниэлу Колин в моей книге использует настоящие математические формулы. Я попросил Дэниэла написать приложение о математических основаниях теоремы Колина. Это приложение, как и любые другие приложения, читать совершенно не обязательно. Но оно жутко интересное. Вам понравится.

Озарение Колина имеет три составляющие.

Во-первых, он заметил, что отношения – это такая штука, для которой можно построить график; один из таких графиков приведен ниже.

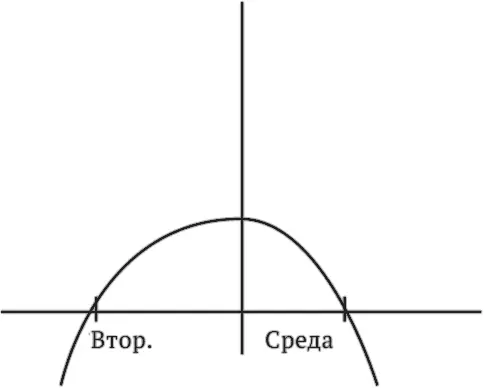
Согласно теории Колина, горизонтальная линия (называемая осью Х) обозначает время. Первый раз, когда кривая пересекает ось Х, – это начало отношений, а когда второй – расставание. Если в промежутке кривая проходит над осью X (как в нашем примере), значит, девочка бросает мальчика; если же кривая проходит под осью X, это означает, что мальчик бросает девочку. («Мальчик» и «девочка» в нашем случае – обозначения условные; в случае однополых отношений, они могут быть «мальчик 1» и «мальчик 2», или «девочка 1» и «девочка 2».) На нашем графике пара впервые целуется во вторник, и девочка бросает мальчика в среду. (В целом, вполне типично для романа между Колином и Катериной.)

Поскольку кривая пересекает ось X только в начале и конце отношений, то, чем дальше проходит кривая от оси, тем дальше момент расставания, или, говоря иначе, тем лучше развиваются отношения.

Вот более сложный пример, график моего романа с одной из моих бывших.

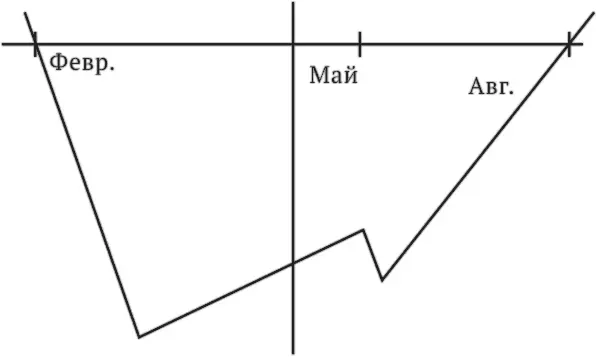
Первый всплеск произошел в феврале, когда через считаные часы после нашей встречи вдруг началась метель и она, разбив машину на заледеневшей дороге, сломала руку. Нам пришлось запереться в моей квартире. Она глотала обезболивающие, а я пытался сжиться с новыми для себя ролями медбрата и бойфренда, что основательно вскружило мне голову. Но этот период закончился внезапно, когда, две недели спустя, снег растаял, рука зажила, и, выбравшись из моей квартиры во внешний мир, мы немедленно обнаружили, что у нас совершенно разный образ жизни и не так уж много общего.

Следующий, менее сильный всплеск произошел, когда мы поехали отдыхать в Будапешт. Отдых быстро подошел к концу, когда мы заметили, что наши романтические каникулы состоят из того, что мы примерно двадцать три часа в день ссоримся из-за мелочей.

Кривая наконец пересекает ось X в августе, когда я бросил ее и она ровно в полночь выставила меня, бездомного и нищего, из квартиры на улицы Беркли.

Второй ингредиент озарения Колина – тот факт, что графики (в том числе и графики романтических отношений) можно представить в виде функций. Сейчас я объясню, потерпите.

Во-первых, когда мы рисуем подобную диаграмму, то

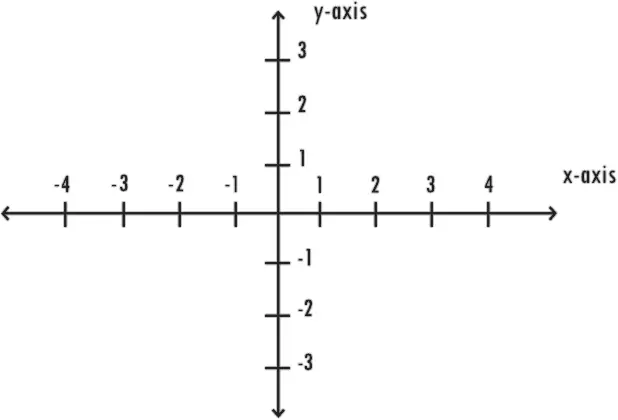
каждую точку на ней можно представить в виде чисел. Отметим числа на горизонтальной (ось X) и на вертикальной (ось Y) оси. Теперь, чтобы обозначить точку на плоскости, нам достаточно указать два числа: одно, указывающее на расстояние от точки до оси X, и второе – до оси Y. Например, точка (2,1) находится около точки (2) на оси X и точки (1) на оси Y. Иначе говоря, она находится на два пункта правее и на один пункт выше точки пересечения осей X и Y, которая обозначается (0,0). Точка (0, -2) расположена на оси Y на два пункта ниже точки пересечения осей, а точка (-3, 2) – на три пункта левее и на два пункта ниже точки пересечения осей.

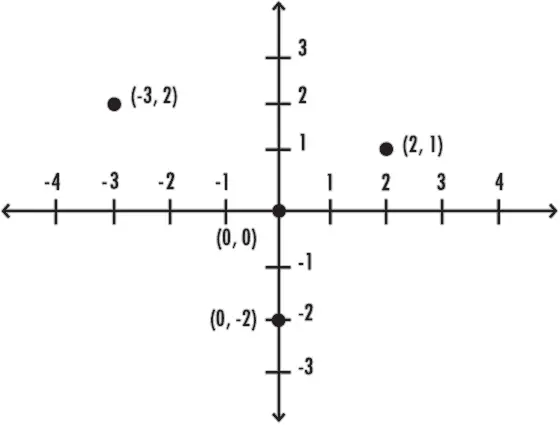
Теперь поговорим о функциях. Функция – это нечто вроде машины, превращающей одни числа в другие. Это правило очень простой игры: я даю вам одно число, а вы возвращаете мне другое.