Джон Грин - Многочисленные Катерины

Например, функция может сказать: «Возьмите число и умножьте его на него же» (то есть возведите в квадрат). Тогда наш диалог будет примерно таким.

Я: 1

Вы: 1

Я: 2

Вы: 4

Я: 3

Вы: 9

Я: 9 252 459 984

Вы: 85 608 015 755 521 280 256

Многие функции можно представить в качестве алгебраических уравнений. Например, функцию, о которой шла речь выше, можно записать так:

Это означает, что я даю вам число x, а вы умножаете его на него же (возводите в квадрат) и возвращаете получившееся число мне. Используя эту функцию, мы сможем отметить все точки вида (x,f(x)). Вместе эти точки образуют некую кривую на плоскости, и мы называем эту кривую «графиком функции». Возьмем функцию

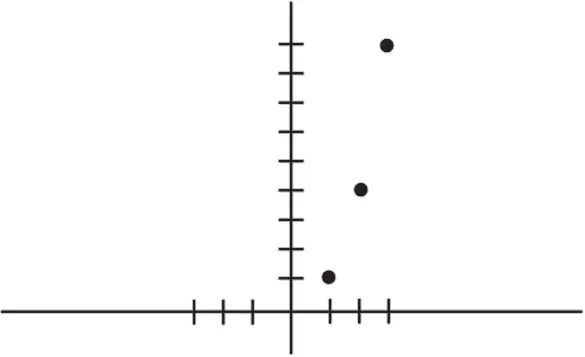
Отметим точки (1, 1), (2, 4) и (3, 9). Также отметим (0, 0), (-1, 1), (-2, 4) и (-3, 9). (Помните, что если отрицательное число умножить на это же число, получится число положительное.)

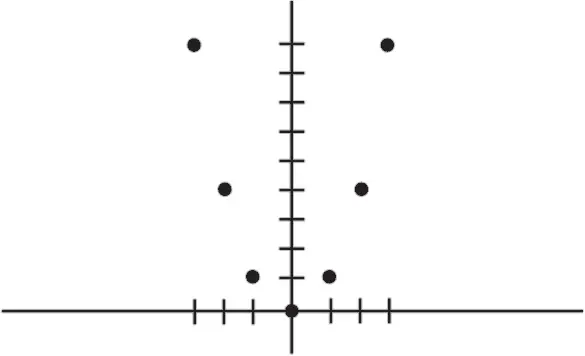
Как вы, наверное, уже догадались, график будет иметь вид вот такой кривой:

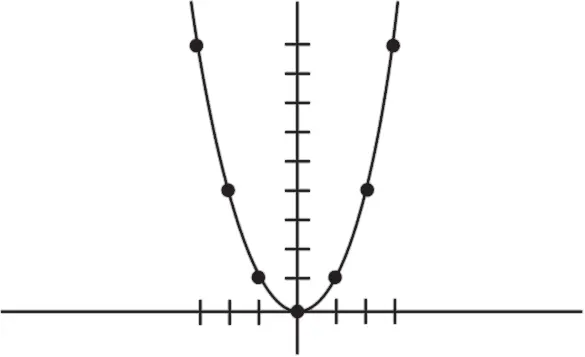
Вы могли заметить, что этот график, к сожалению, довольно плохо годится для отображения отношений. Графики, которые Колин использует для своей теоремы, должны пересечь ось Х дважды (в первый раз – когда пара начинает встречаться, и во второй – в момент расставания), а наш график коснулся ее только единожды. Но это можно легко исправить, используя чуть более сложные функции. Возьмем, например, функцию:

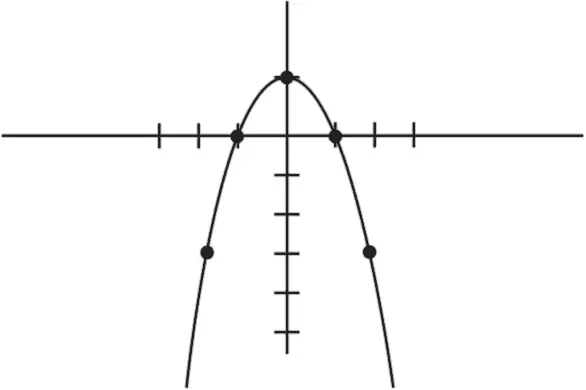
График Колину знаком – это график короткого романа, который завершается тем, что его бросает девочка (нам известно, что девочка бросает Колина, потому что в промежутке между первым поцелуем и расставанием график проходит над осью Х). В общих чертах этот график верно описывает историю жизни Колина. Теперь остается только немного подправить ее, чтобы уточнить детали.

Одно из главнейших направлений математики в двадцатом веке – изучение семейств объектов. (Когда математики говорят «семейство», они имеют в виду «любое количество сходных объектов». Например, стул и стол принадлежат к семейству «мебель».)

Вот в чем идея: линия – это не более чем множество (семейство) точек; плоскость – семейство линий и так далее. Это аргумент в пользу того, что если вам интересен один объект (например, точка), то еще интереснее будет изучать все семейство сходных объектов (например, линию). В последние шестьдесят лет этой точки зрения придерживаются все ведущие математики мира.

Самое время поговорить о третьем кусочке пазла под названием «Эврика, или Озарение Колина». Каждая Катерина уникальна, и каждая из них бросает Колина уникальным образом. Это означает, что, как бы тщательно Колин ни работал над усовершенствованием одной функции или одного графика, результат будет касаться только одной Катерины. На самом деле Колину нужно изучить всех возможных Катерин со всеми их функциями. Другими словами, ему нужно исследовать все семейство функций Катерин.

Итоговое открытие Колина таково: романтические отношения можно отобразить на графике, а графики – это отображения функций, и все эти функции можно свести к одной (очень сложной) формуле, которая позволит ему предсказать, когда его бросит следующая Катерина (и, что важнее, бросит ли она его вообще) [89].

Давайте я объясню на примере, что это значит. Возьмем первую формулу Колина. Она выглядит так:

Для того чтобы ее объяснить, мне предстоит ответить на множество вопросов.

Во-первых, что такое D? Это дифференциал Бросальщика/ Брошенного: число, определяющее, где находится человек на нашей Шкале Разбитых Сердец.

Если вы пытаетесь предсказать, как будут развиваться отношения между мальчиком и девочкой, вы берете дифференциал Б/Б мальчика и вычитаете из него дифференциал Б/Б девочки. (Если дифференциал Б/Б мальчика = 2, а дифференциал Б/Б девочки = 4, то мы получим D = минус 2.)

Теперь посмотрим, как это отразится на графике. В вышеприведенном примере мы имеем функцию

график которой выглядит так:

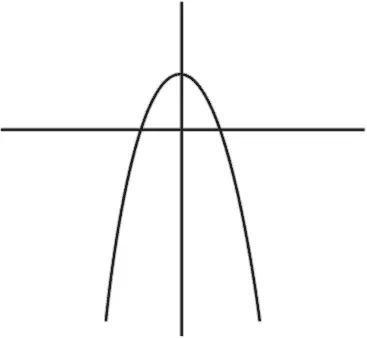
Как видите, роман длится недолго, и девочка бросает мальчика (ситуация, знакомая Колину).

Если же дифференциал Б/Б мальчика = 5, а дифференциал Б/Б девочки = 1, то мы получим D = 4 и функцию

с таким графиком:

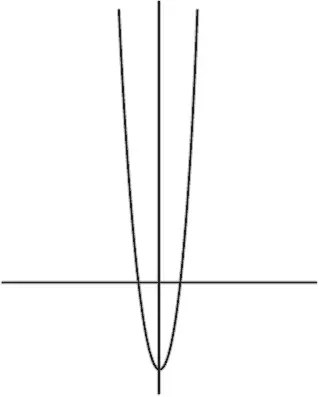
Этот роман – еще короче, но, судя по всему, еще напряженней (вершина очень крутая), и на этот раз мальчик бросает девочку. К сожалению, у этой формулы есть изъяны. Во-первых, если D = 0, то есть пара имеет одинаковый результат на Шкале Разбитых Сердец, то мы получим функцию

график которой – простая горизонтальная линия, и по ней невозможно определить, когда отношения начинаются или заканчиваются.

Главная проблема в том, что совершенно абсурдно думать: отношения настолько просты, что их графики совершенно однотипны, – и именно это Линдси Ли Уэллс помогает Колину понять. И итоговая формула Колина гораздо сложнее.

Но уже здесь заметно главное: поскольку D может быть разным, эта формула описывает целое семейство функций, каждая из которых, в свою очередь, описывает отношения с одной из Катерин. Так что Колину осталось только добавить больше переменных (ингредиентов вроде D) в эту формулу, чтобы она описывала более обширное семейство функций и, возможно, смогла бы охватить весь сложный и труднопредсказуемый мир расставаний с Катеринами. Именно это Колину и помогает понять Линдси.

Такова история Колина Одинца, его Эврики и Теоремы Предсказуемости Катерин. Должен заметить, что хотя ни один разумный взрослый математик (по крайней мере, тот, у кого есть сердце) не станет всерьез утверждать, что развитие романтических отношений можно предсказать с помощью единственной формулы, в последнее время над этим вопросом кое-кто задумывался. Говоря точнее, психолог Джон Готтман (долгое время возглавляющий «Лабораторию любви» Вашингтонского университета) вместе с математиком Джеймсом Мюрреем и другими соавторами написал книгу «Математика брака», в которой сделана попытка математическими методами предсказать, распадется ли брак [90]. В общих чертах идея напоминает теорему Колина, но математически она гораздо более сложна, а итоговый результат – гораздо более скромен (авторы не берутся предсказать каждый развод, а просто делают некоторые обоснованные предположения) [91].