Александра Малова - Основы эконометрики в среде GRETL. Учебное пособие

В появившемся диалоговом окне в поле Зависимая переменная помещаем переменную 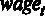(для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная . Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).

Для дальнейшего удобства можно поставить галочку в окошке Установить по умолчанию . Это делается для того, чтобы при изменении спецификации исследуемой модели зависимая переменная не менялась. В окно Регрессоры отправляем регрессоры модели – это переменные , , .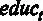

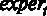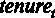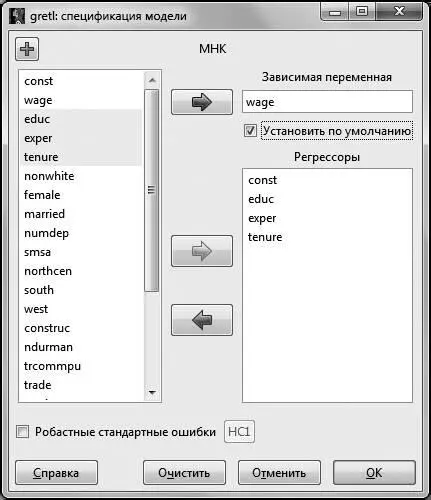
Рис. 2.1

После этого нажимаем ОК . В результате коэффициенты модели были оценены методом наименьших квадратов. Результат оценки представлен на рис. 2.2.

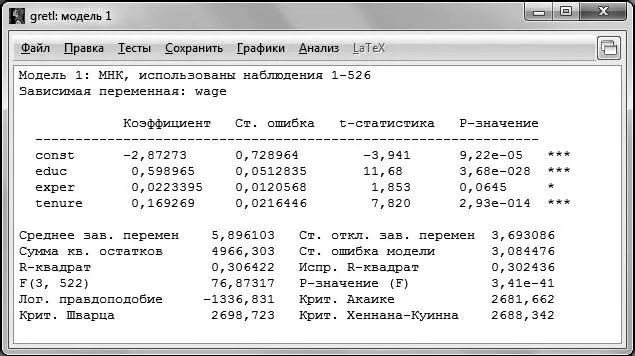
Рис. 2.2

Для того чтобы понимать, какие результаты позволяет получить GRETL, разберем информацию, представленную на распечатке по строкам сверху вниз.

В первой строке указывается метод оценки и количество наблюдений, по которым производилась оценка. Достаточно часто случается, что количество наблюдений, по которым производилась оценка, не совпадает с числом наблюдений в исходной выборке, даже если она не была ограничена. Это может быть связано, например, с наличием пропусков в данных.

Вторая строка напоминает нам о том, какая переменная была выбрана в качестве зависимой.

После двух первых строк следуют подтаблицы непосредственно с результатами оценивания. В первой подтаблице указаны регрессоры, включенные в модель, напротив каждого из них указывается его коэффициент (столбец Коэффициенты ), стандартная ошибка оценки коэффициента (столбец Ст. ошибка ), значение статистики Стьюдента для коэффициента (столбец t-статистика ) и вероятность ошибки I рода (столбец P-значение ). Стоит отметить, что константа тоже является регрессором, и для нее также рассчитываются все указанные характеристики.

По распечатке, представленной на рис. 2.2, мы можем выписать получившееся уравнение регрессии:

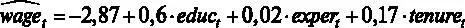
Аналогично можно получить оцененное уравнение и в GRETL, для этого выбираем в меню регрессии Файл – Просмотреть как уравнение.

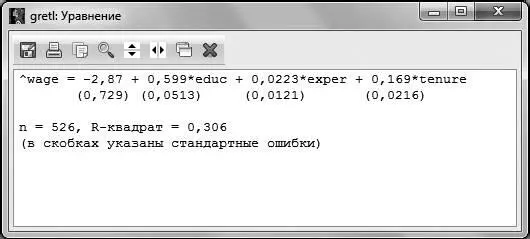
Рис. 2.3

Однако для того, чтобы иметь возможность дать интерпретацию коэффициентам регрессии и строить прогнозы, необходимо проверить, является ли полученная модель адекватной.

Для этого, в свою очередь, необходимо провести ряд эконометрических тестов, а именно проверить значимость регрессии в целом, значимость отдельных коэффициентов регрессии, оценить качество полученного регрессионного уравнения. Вообще говоря, перед проверкой значимости и качества уравнения необходимо провести тесты на выполнение основных предпосылок линейной регрессионной модели (гомоскедастичность, отсутствие автокорреляции). На данном этапе мы будем считать эти тесты проведенными и вернемся к вопросам выполнения предпосылок ЛРМ позднее.

Для начала проверим гипотезу о незначимости регрессии в целом. Тест позволит понять, является ли построенная модель адекватной с точки зрения статистики. Для этой цели воспользуемся тестом Фишера [3].

Сформулируем гипотезы для проверки незначимости регрессии в целом в рассматриваемом примере [ файл с данными wage1.gdt ] модели , :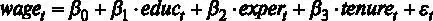

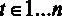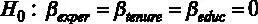
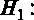как минимум один из коэффициентов отличен от нуля.

Для принятия решения о том, какую гипотезу нужно отвергнуть, построим F- статистику. Для этого нам должны быть известны (помимо уже имеющихся параметров n – объем выборки и k – число регрессоров в модели) величины RSS и ESS . В явном виде в распечатке на рис. 2.2 дано значение ESS – сумма квадратов остатков, которая составляет ESS = 4966,3, а также из распечатки известен коэффициент детерминации 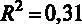(подробнее о коэффициенте детерминации и его интерпретации можно прочесть в § 7).

Если вспомнить, что 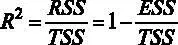, 1а 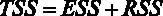, то можно путем простых алгебраических преобразований найти необходимую нам величину RSS . При этом 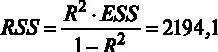. Отсюда можно вычислить 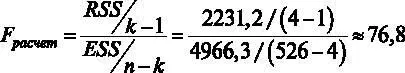. Критическое значение F- статистики возьмем на уровне значимости 5 %: 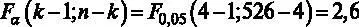(чтобы получить это значение, в основном меню GRETLнужно выбрать Инструменты – Критические значения – Фишера и ввести необходимое число степеней свободы и правостороннюю вероятность либо посмотреть в статистических таблицах распределения Фишера для уровня значимости 5 %, например в [7]).

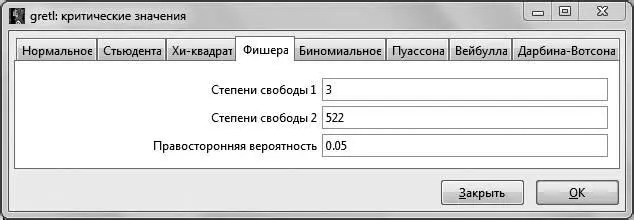
Рис. 3.1

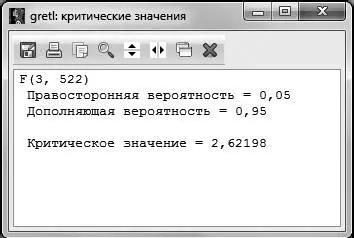
Рис. 3.2