Александра Малова - Основы эконометрики в среде GRETL. Учебное пособие

Данный тест можно проводить несколькими способами в GRETL, рассмотрим каждый из них на примере рассматриваемой модели.

Сформулируем гипотезу о совместной незначимости регрессоров , .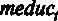

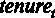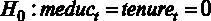
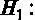
не так

Результаты оценивания регрессии без ограничения приведены на рис. 5.1, сумма квадратов остатков данной модели .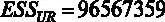

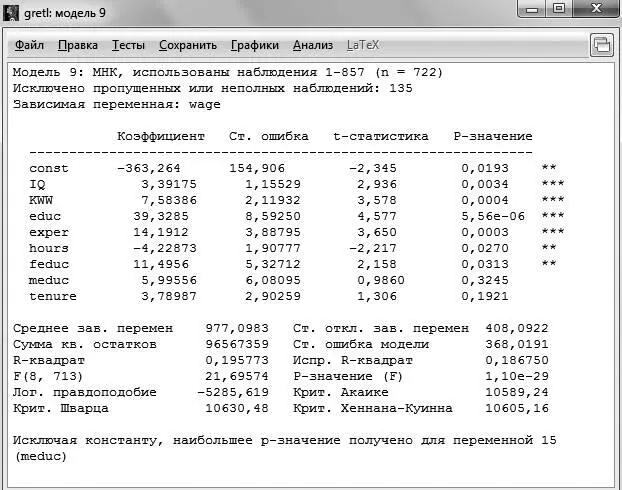
Рис. 5.1

Оценим регрессию с ограничением, то есть исключим из нее переменные с коэффициентами, подозрительными на совместную незначимость. Для этого можно, очевидно, по новой оценить модель, но можно и в существующей модели выбрать пункт меню Правка – Изменить модель и удалить регрессоры с коэффициентами, подозрительными на совместную незначимость. Результат оценивания модели с ограничением представлен на рис. 5.2.

Сумма квадратов остатков в модели с ограничением .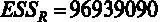

Далее рассчитаем значение F- статистики:

Критическое значение статистики составляет 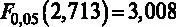, таким образом, 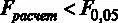, гипотеза о совместной незначимости коэффициентов при этих регрессорах на 5 %-ном уровне значимости принимается. Оба регрессора могут быть исключены из модели, и тогда окончательной спецификацией будет модель с ограничением:

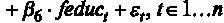
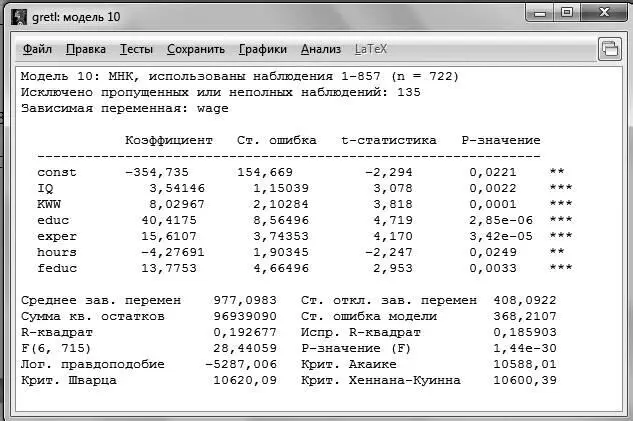
Рис. 5.2

Тест на совместную незначимость коэффициентов также можно провести автоматически. Для этого, после того как было оценено исходное уравнение, в меню окна результатов нужно выбрать Тесты – Избыточные переменные .

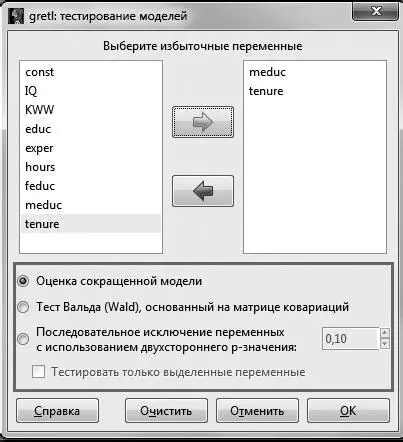
Рис. 5.3

После этого в меню можно выбрать одну из опций оценивания: оценить сокращенную модель (аналог того теста, который был показан выше) или проверить избыточность переменных с использованием теста Вальда [9].

Результат оценивания с использованием сокращенной модели представлен на рис. 5.4.

Рис. 5.4

При данном методе проверки также рассчитывается F- статистика и ее значение совпадает с тем, что было получено вручную. При этом приводится оцененный вариант короткой модели (модели с ограничением). Нулевая гипотеза состоит в том, что указанные на этапе тестирования переменные 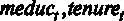нулевые. Для проверки этой гипотезы можно воспользоваться рассчитанным значением F- статистики и сравнить его с критической точкой, как это было проделано, а можно обратить внимание на р- значение = 0,254184, то есть вероятность ошибиться, отвергнув нулевую гипотезу о незначимости коэффициентов, составляет примерно 0,26. Так как р- значение > 0,05 (больше зафиксированного уровня значимости), мы принимаем нулевую гипотезу, указанные коэффициенты не значимы на 5 %-ном уровне, и соответствующие регрессоры нужно исключить из модели. Корректный вариант модели – модель с ограничением.

Аналогично можно провести тест на избыточные переменные, используя тест Вальда (рис. 5.5).

Рис. 5.5

Результаты тестирования полностью совпадают с предыдущими вариантами теста.

Для проверки правильности спецификации линейной регрессионной модели используется RESET-тест. Он позволяет определить, помогает ли нелинейная комбинация оцененного значения зависимой переменной лучше объяснить изменения самой зависимой переменной. Если качество объяснения при этом улучшается, значит, модель специфицирована неправильно [9].

Проведем RESET-тест для модели

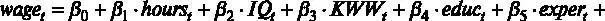
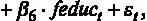
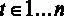
то есть проверим правильность спецификации этой модели [ файл с данными wage2.gdt ]. Оценим предложенную регрессию и сохраним оцененные значения зависимой переменной. Для этого в окне с результатами оценки выберем пункт меню Сохранить – Расчетные значения.

Рис. 6.1

После этого включим степени расчетных значений зависимой переменной в качестве регрессоров. Как правило, число степеней может равняться числу регрессоров в исходной модели, но начинать можно и с меньшего количества. Добавить новые переменные (степени расчетных значений зависимой переменной) можно через основное меню Добавить – Добавить новую переменную и ввести формулу, можно для четных степеней воспользоваться функцией меню Добавить – Квадраты выделенных переменных , а можно прямо в окне для оценки регрессии выбрать кнопку (+), которая позволит тут же создать новую переменную.