Александра Малова - Основы эконометрики в среде GRETL. Учебное пособие

Проверить, может ли коэффициент при регрессоре равняться заданному значению, позволяет также доверительный интервал [2, 3].

Используя данные из распечатки на рис. 4.6, можно построить доверительные интервалы для всех коэффициентов самостоятельно либо воспользоваться встроенной функцией GRETLдля построения доверительного интервала.

Для этого в окне модели вызовем пункт меню Анализ – Доверительные интервалы для коэффициентов.

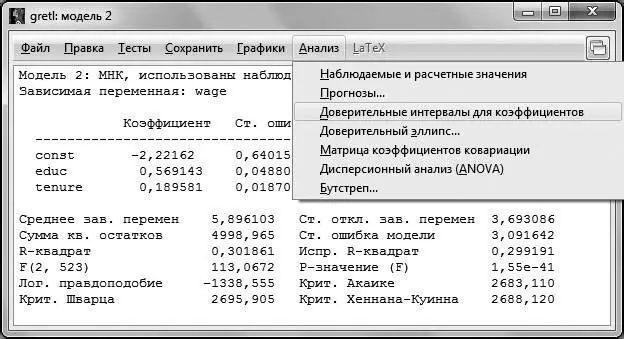
Рис. 4.7

Результатом работы данной функции является следующее окно (рис. 4.8).

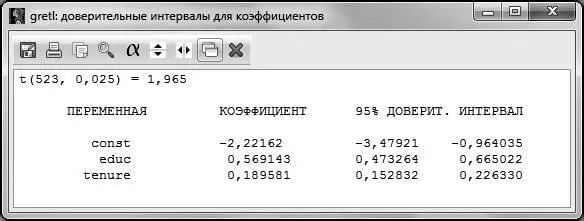
Рис. 4.8

Истинное значение коэффициента при переменной 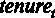с вероятностью 95 % накрывается интервалом .

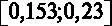Нужно обратить внимание на то, что с помощью доверительного интервала можно проверять незначимость коэффициентов при регрессорах. В случае, если доверительный интервал накрывает 0 (то есть истинное значение коэффициента может принимать нулевое значение), можно сделать вывод о том, что коэффициент не значим.

Еще одна возможность для проверки гипотез с помощью теста Стьюдента – это односторонние гипотезы [2, 3].

Разберем, как проводится односторонний t -тест на примере. Проверим, верно ли, что коэффициент перед переменной 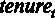можно считать большим 0,2.

Значение расчетной статистики для этого теста будет такое же, как и в предыдущем тесте (проверка равенства коэффициента заданному значению). Критическая точка составит . Сравнивая расчетное значение статистики с критическим, получаем 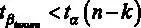, то есть –0,56 < 1,65. Значит, гипотеза H 0принимается.

По сути, все разновидности t- теста и построение доверительного интервала для коэффициента – это две стороны одной медали. Полезные результаты можно получать и тем и другим способом, выбор способа ответа на вопросы о незначимости коэффициента при регрессоре и соотношения коэффициента регрессора с заданным значением возлагается на исследователя.

В рассматриваемой нами модели зависимости заработной платы после проверки незначимости коэффициентов при отдельных регрессорах осталось две независимых переменных: образование и опыт работы у текущего работодателя. Однако с экономической точки зрения очевидно, что на уровень заработной платы сотрудника могут влиять и некоторые другие факторы, например, уровень интеллекта (IQ), возраст, образование и заработок родителей, общий уровень знаний и проч. Когда мы отбираем регрессоры для модели, мы, с одной стороны, должны руководствоваться соображениями экономической обоснованности и осмысленности, а с другой – нужно иметь в виду и эконометрические аспекты. Так, например, нужно помнить, что если не включить существенные регрессоры в модель, оценка для дисперсии ошибок модели получится смещенная, и тогда тесты на незначимость будут работать некорректно. Если же включить несущественную переменную, оценки для коэффициентов хоть и будут несмещенные, но получатся неэффективными. Таким образом, отбирая регрессоры для модели, нужно учитывать как содержательные аспекты, так и эконометрические.

Предположим, что с точки зрения экономического смысла мы определились с регрессорами и решили построить следующую модель [ файл с данными wage2.gdt ]:

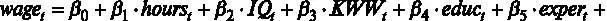
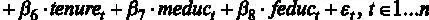
где 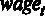– средняя заработная плата в месяц в долларах, 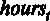– среднее число рабочих часов в неделю, 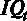– уровень IQ в баллах, 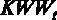– индекс знания своей области деятельности в баллах, 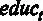– уровень образования в годах, 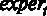– опыт работы в годах, 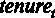– опыт работы у текущего работодателя в годах, 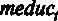– образование матери, 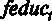– образование отца 2.

На рис. 5.1 дана распечатка оцененной регрессии. По распечатке можно сделать вывод, что в целом регрессия значима, но не все коэффициенты значимы по отдельности.

На 5 %-ном уровне значимости сразу несколько коэффициентов перестают быть значимыми. Если бы не значим был лишь один коэффициент в модели, его можно было бы исключить, но в случае незначимости нескольких коэффициентов можно ли исключить соответствующие регрессоры из модели на том основании, что коэффициент каждого из них в отдельности не значим на 5 %-ном уровне? Чтобы ответить на этот вопрос, нужно вспомнить о том, что существенные регрессоры исключать из модели некорректно, но оставлять несущественные регрессоры в модели тоже не является правильным. Поэтому для того, чтобы понять, можно ли исключить все регрессоры, чьи коэффициенты не значимы на 5 %-ном уровне, или нужно исключить только некоторые из них и какие именно, необходимо провести тест на совместную незначимость коэффициентов при регрессорах [2, 3].