Александра Малова - Основы эконометрики в среде GRETL. Учебное пособие

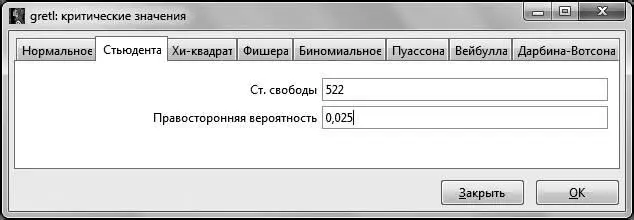
Рис. 4.2

Стоит обратить внимание на то, что в GRETLпредполагается для распределения Стьюдента вводить не двустороннюю вероятность, а только правостороннюю вероятность, то есть в нашем случае это 2,5 %. После нажатия клавиши ОК получаем искомое критическое значение .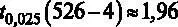

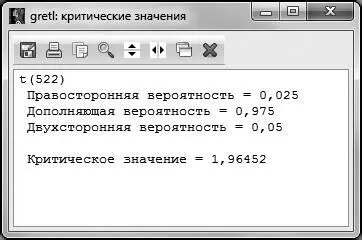
Рис. 4.3

После этого сравниваем расчетное и критическое значение статистик для переменной 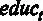. В нашем случае 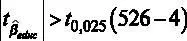(|11,68 | > 1,96), отсюда можно сделать вывод, что гипотеза H 0отвергается, то есть можно говорить о том, что регрессор 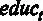значим.

Рассмотренный способ проверки гипотезы незначимости коэффициента при отдельном регрессоре позволяет соотнести теоретические знания о проверке незначимости с практикой. Однако ту же самую процедуру можно несколько упростить. Обратим внимание, что в столбце t- статистика для всех переменных уже указаны расчетные значения статистики. Так, например, для переменной 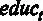указано полученное нами значение 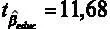. Это несколько сокращает процедуру проверки, однако сравнение расчетного и критического значения t- статистики все же приходится проделывать самостоятельно.

Существует еще более простой и быстрый способ проверки незначимости коэффициента.

В рассматриваемом примере p- значение переменной 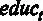составляет 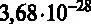, то есть практически равно 0. В этом случае, p- значение переменной 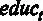меньше заданного уровня значимости 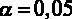. Это значит, что можно отвергнуть гипотезу H 0, то есть коэффициент при регрессоре 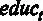значим.

Аналогичную проверку незначимости мы можем провести для коэффициентов остальных регрессоров. На 5 %-ном уровне значимости можно утверждать, что коэффициент при 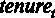и константа – значимы, коэффициент при 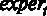на 5 %-ном уровне не значим, однако он является значимым на 10 %-ном уровне значимости.

В программе GRETLпредусмотрена визуализация значимости коэффициентов при отдельных регрессорах на разных уровнях значимости. Для этого справа от каждого регрессора расположены звездочки:

• Наличие одной звездочки говорит о том, что коэффициент значим только на 10 %-ном уровне.

• Наличие двух звездочек говорит о значимости коэффициента на 5 %-ном уровне.

• Три звездочки информируют о значимости коэффициента на 1 %-ном уровне.

• Отсутствие звездочек говорит о незначимости коэффициента на 10 %-ном уровне.

Мы проверили незначимость коэффициентов при всех регрессорах, включенных в модель. Если мы хотим ориентироваться на 5 %-ный уровень значимости, то нужно удалить переменную с незначимым коэффициентом. Для того чтобы это сделать в окне с построенной моделью (в нашем случае это окно Модель 1, но, вообще говоря, это может быть Модель № в зависимости от того, сколько вы моделей построили до этого), выбираем пункт меню Правка – Изменить модель .

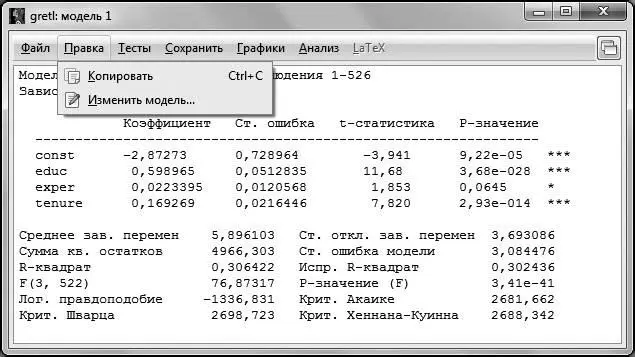
Рис. 4.4

В открывшемся окне выделяем переменную и красной стрелкой удаляем ее из независимых переменных.

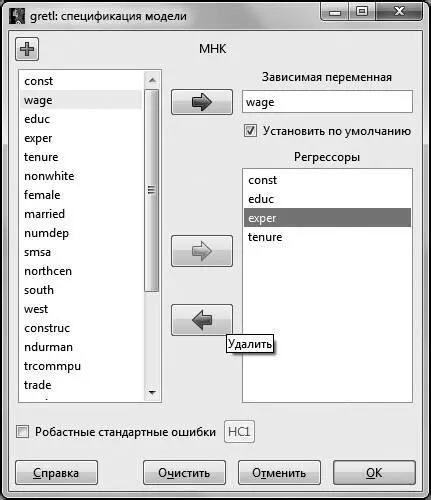
Рис. 4.5

Обновленная модель представлена на рис. 4.6.

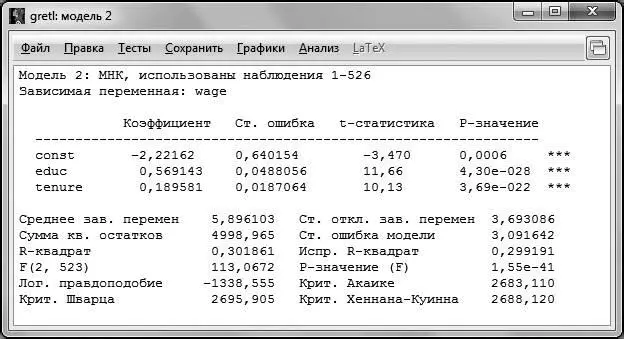
Рис. 4.6

Как видно из распечатки, все коэффициенты регрессии в обновленной модели значимы на 1 %-ном уровне (следовательно, и на 5 %-ном уровне они тоже значимы). Возможности t- теста не ограничиваются только проверкой незначимости коэффициентов при регрессорах. На самом деле проверка незначимости коэффициента является частным случаем проверки равенства коэффициента при регрессоре конкретному значению [2, 3].

Разберем это на примере. Проверим, а можем ли мы округлить коэффициент при переменной 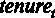до 0,2. Сформулируем гипотезы для проверки этого предположения:

Для проверки такого рода гипотезы уже нельзя воспользоваться рассчитанным в GRETLзначением t- статистики, а также р- значением, поэтому вычислим значение t- статистики для переменной 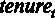самостоятельно: . Значение критической точки Стьюдента составит .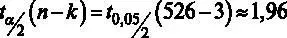

Сравниваем расчетную статистику и критическую и получаем, что 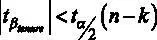, то есть (|–0,56 | < 1,96). В этом случае, мы можем принять нулевую гипотезу и округление коэффициента перед 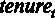до 0,2 будет статистически корректно. Аналогичные гипотезы мы можем проверять для остальных коэффициентов регрессии.