Александр Волошинов - Математика и искусство

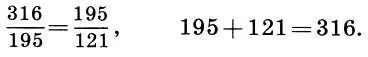
Но на этом чудеса гениального творения Баха только начинаются. Построив ряд золотого сечения (12.4) при а = 316, имеем

316 195,3 120,7 74,6 46,1 28,5 17,6.

Каково же должно быть наше удивление, когда мы обнаружим, что на 124-й четверти находится кульминация первой части и стоит знак ферматы, а на 77-й четверти от начала второй части имеет место кульминация второй части! Таким образом, кульминация обеих частей с небольшой погрешностью, легко объяснимой растяжимостью темпов, делит эти части по закону золотого сечения. Далее, каждый из полученных четырех разделов Хроматической фантазии имеет характерные особенности, которые также с потрясающей точностью приходятся на точки золотого деления этих разделов! Наконец, Розенов нашел и более мелкие деления Хроматической фантазии в золотой пропорции, на которых мы не будем останавливаться.

Итак, Хроматическая фантазия, произведение свободного по форме жанра, буквально соткано из золотых пропорций! Пожалуй, эстетическое впечатление от математического анализа Хроматической фантазии имеет не меньшую силу, чем прослушивание бессмертного творения Баха. А взятые вместе — чувственное впечатление и рациональный анализ, безусловно, позволяют еще на один шаг приблизиться к сокровенным тайникам гения.

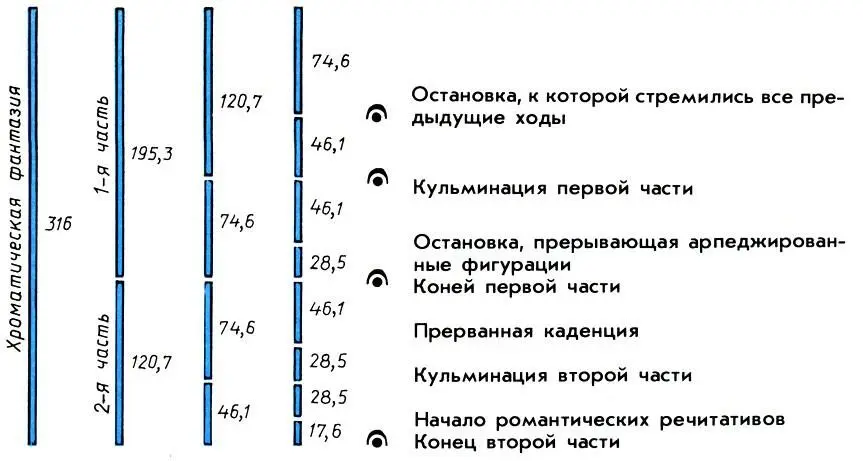
Главные золотые сечения Хроматической фантазии И. С. Баха. Цифры обозначают число четвертей теоретического ряда золотого сечения (а = 316). Справа дано описание соответствующих характерных мест нотного текста фантазии

Перейдем к анализу фуги. Фуга (от лат. fuga — бег) является наиболее совершенной формой многоголосной музыки (полифонии). Фуга строится на многократных проведениях (повторениях) основной музыкальной темы в разных голосах. Проведения основной темы обычно перемежаются в фуге с промежуточными вставками, называемыми интермедиями . Таким образом, фуга в отличие от фантазии имеет четко определенный закон построения. Но тем не менее точность "математического" построения фуги ре минор просто поражает!

Фуга ре минор состоит из семи пар проведений и интермедий и двух самостоятельных проведений. Из семи пар "проведение-интермедия" пять пар строго подчиняются закону золотого сечения. Те же две пары "проведение-интермедия", для которых закон золотого деления не выполнен, являются своеобразными центрами симметрии относительно обрамляющих их разделов фуги и с каждым из них находятся в золотой пропорции! Именно для того, чтобы выделить эти два центра симметрии, Бах специально допускает в их строении отклонения от золотого деления и делает эти две пары "проведение-интермедия" симметричными.

На рисунке приведена схема строения фуги ре минор. Здесь же указано число четвертей в каждом разделе фуги (целые числа) и даны теоретические значения членов золотой пропорции (дробные числа). Как видим, все пять пар "проведение-интермедия" с изумительной точностью разделены в золотой пропорции (абсолютные ошибки колеблются в диапазоне от 0,05 до 0,15 четверти, относительные ошибки — от 0,02% до 0,7%). Таким относительным погрешностям могут позавидовать многие из современных инженерных расчетов! В более крупных разделах абсолютные ошибки, естественно, возрастают. Но и при делении самого большого раздела (91 четверть) эти ошибки не превышают 1,25 четверти. Не следует, однако, забывать, что мы имеем дело с художественным произведением. Отметим, что в фуге ре минор существуют также и более мелкие, и более крупные соотношения золотого сечения, на которых мы просто не останавливаемся.

Итак, простой математический анализ, не выходящий за рамки арифметики, позволяет совершенно иными глазами взглянуть на музыкальное произведение, увидеть его скрытую внутреннюю красоту, которую мы только ощущаем, слушая произведение, и которую мы "видим", проводя его математический анализ. Вот как сказал об этом Розенов: "При взгляде на схемы Хроматической фантазии и фуги... невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силой художественной чуткости до такой степени точности законы природного творчества".

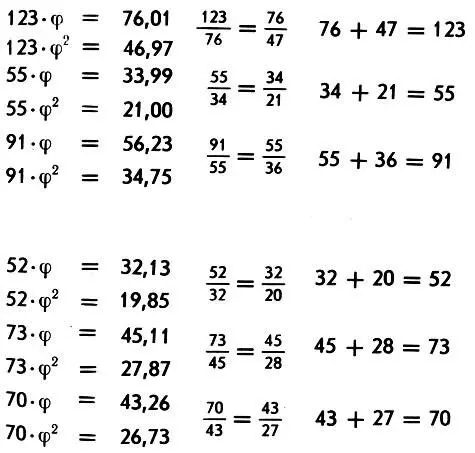
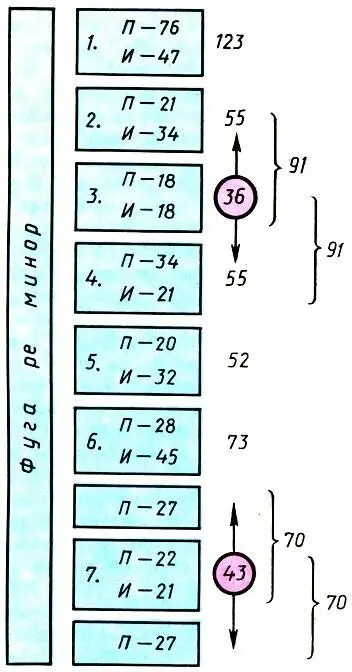
Строение фуги ре минор И. С. Баха. Целые числа указывают число четвертей в фуге, дробные — теоретические значения золотых сечений. Золотые пропорции в более крупных частях фуги отмечены фигурными скобками, центры симметрии — кружками. П — проведение, И — интермедия

Далее Розенов, "дабы показать, что приведенный пример не является у Баха исключительным", рассматривает многочисленные прелюдии и фуги из "Хорошо темперированного клавира" Баха, а также оперу Моцарта "Дон-Жуан", финал знаменитой "Лунной" сонаты Бетховена, Фантазию фа минор Шопена, вступление к опере "Тристан и Изольда" Вагнера, увертюру к опере "Руслан и Людмила" Глинки и многие народные песни. Во всех этих произведениях Розенов с замечательной точностью обнаруживает действие закона золотого сечения. "Приведенные мною примеры проявления закона золотого сечения настолько характерны и замечательны,- пишет Розенов,- что исключают всякую возможность отрицания эстетического значения этого закона в музыке". Не правда ли, здесь мы имеем тот самый случай, когда "цифры могут представлять собой культурную и эстетическую ценность"? (См. высказывание Н. Винера в эпиграфе к первой части книги.)

Но помимо установления самого факта наличия закона золотого сечения в музыкальных произведениях и его огромного эстетического значения в музыке математический анализ музыки (даже такой элементарный) позволяет сделать некоторые выводы о характерных особенностях творчества самих композиторов. Так, сравнивая проявление закона золотого сечения у Баха и Бетховена, Розенов пишет: "Мы находим у Баха сравнительно более детальную и органическую сплоченность. Закон золотого деления проявляется у него с поразительной точностью в соотношениях крупных и мелких частей как в строгих, так и в свободных формах, что, несомненно, соответствует с характером этого гениального мастера-труженика, сильным, здоровым и уравновешенным, с его глубоко сосредоточенным отношением к работе и детально отделанной манерою письма. У Бетховена проявление закона золотого сечения глубоко логично по отношению к размерам частей формы, но главным образом указывает на силу темперамента этого автора по точности совпадения всех моментов высшего напряжения чувств и разрешения подготовленного ожидания с моментами золотых сечений. У Шопена внутренняя формальная связь сравнительно слабее и проявляется не сплошь, а лишь местами. По силе темперамента он сходен с Бетховеном, но проявление это более внешне и касается чаще изящной нарядности изложения мысли, нежели его внутренней логики. У Моцарта темперамент проявляется сравнительно слабее, закон золотого сечения направлен у него особенно часто к подчеркиванию драматических элементов (психологических контрастов, противопоставлений характеров) и трагических положений. У Глинки мы находим применение данного закона только лишь в широких масштабах при полном почти отсутствии мелочных соответствий, встречающихся так часто у Баха и Шопена".