Александр Волошинов - Математика и искусство

Вот к каким глубоким эстетическим выводам приводит простейший математический анализ музыки! Слова Розенова о том, что закон золотого сечения "может, по-видимому, явиться в дальнейшем немаловажным вкладом в экспериментальную эстетику", оказались пророческими. А сама экспериментальная эстетика сегодня обрела наконец права гражданства и уверенно набирает силу.

Из начала XX столетия перенесемся теперь в его вторую половину и перейдем к современным исследованиям по экспериментальной эстетике. Начиная с 1952 г. интересные работы по применению математических методов в исследованиях искусства — литературы, живописи, музыки — публикует видный немецкий ученый Вильгельм Фукс. Фукс — прежде всего физик, работающий в области физики плазмы. Однако у этого ученого-энциклопедиста есть и хобби — исследования в области экспериментальной эстетики, часть из которых собрана в интереснейшей монографии Фукса "По всем правилам искусства". В своих работах по экспериментальной эстетике Фукс стремился показать, что точные методы могут быть эффективно применены к исследованию культурного наследия человечества. Хотя со времен Галилея и Ньютона математическое описание стало великим путем познания природы, применение математического метода к искусству до сих пор вызывало недоверие, сарказм или просто неприязнь. Повинна в этом, скорее всего, все та же инерция мышления, "благодаря" которой в свое время отвергались анатомия и демографическая статистика, считавшиеся уделом лишь Бога и короля. Однако, как отмечает Фукс, "выдающиеся успехи точных наук в присущих им сферах привели к тому, что теперь все более соблазнительной представляется идея испытать методы этих наук и в других областях". В силу известного нам свойства математики "называть разные вещи одним и тем же именем" такие исследования помогли бы выявить общие закономерности в разнородных, на первый взгляд, явлениях культуры. Тем не менее сама постановка подобной проблемы была столь нова и необычна, что Фукс вполне справедливо задавал сам себе вопросы: "Можно ли применять абстрактный аппарат точных наук к явлениям культуры? И если да, то имеет ли это смысл? Будут ли получены при этом результаты, столь же объективные, как и в естественных науках? Удастся ли помимо голых чисел, результатов измерений и статистической обработки фактического материала выявить некий род объективных закономерностей, регулярностей, характерных форм явлений?"

Нам представляется, что работы Фукса дали, бесспорно, положительный ответ на эти вопросы, и мы надеемся, что рассматриваемые далее примеры, относящиеся к математическому анализу музыки, будут тому блестящим доказательством.

Вновь обратимся к анализу высоты музыкальных звуков, которому посвящена практически вся вторая часть книги. На примере многочисленных скрипичных произведений Фукс исследовал, как разные авторы в разные эпохи использовали звуковой материал скрипки. Диапазон звучания скрипки простирается от ноты соль малой октавы до ноты до пятой октавы. Считая энгармонически равные звуки ( до-диез = ре-бемоль и т. п.) за один звук, в диапазоне соль-до 5 мы имеем 54 звука. Пронумеруем их, т. е. каждому звуку скрипки поставим в соответствие число i = 1, 2, ..., 54: соль ⇔ i = l, соль-диез = ля-бемоль ⇔ i = , ля ⇔ i = 3 ..., до 5⇔ i = 54. Подсчитав общее число звуков N в данном произведении, легко найти относительную частоту появления i-ro звука по формуле

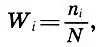
где n i— частота i-то звука, т. е. число появлений i-го звука в произведении. Например, в струнном квартете ми-бемоль мажор Бетховена, в партии первой скрипки N = 3796, а нота соль первой октавы (i = l) встречается 23 раза (n 1=23). Следовательно, ее относительная частота W 1= 23/3796 = 0,006. Ясно, что если самые верхние звуки из диапазона звучания скрипки в произведении не используются, то их частота будет равна нулю. Совокупность (i, W i) i = l, 2, ..., k называется статистическим распределением , а ломаная линия, отрезки которой соединяют точки статистического распределения, называется полигоном относительных частот . Заметим, что поскольку n 1+ n 2+ ... + n k= N, то W 1+ W 2+ ... + W k= (n 1+ n 2+... + n k)/N=l, т. е. сумма всех относительных частот статистического распределения равна 1 .

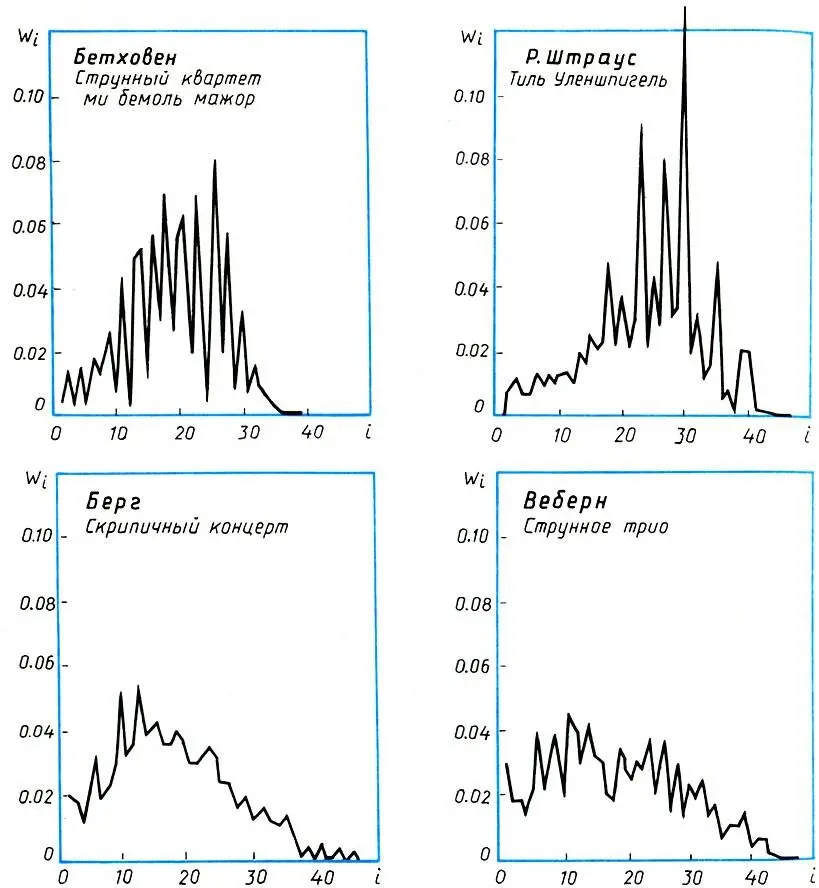
Полигоны относительных частот высоты звуков в партии первой скрипки. Уже по внешнему виду статистических распределений можно заключить, что композиторы-додекафонисты Берг и Веберн применяли совершенно иные правила композиции, чем Бетховен и Рихард Штраус

На рисунке построены полигоны относительных частот высоты звуков в партии первой скрипки для четырех музыкальных произведений: струнного квартета ми-бемоль мажор Бетховена (1809) (партия первой скрипки); симфонической поэмы Рихарда Штрауса "Тиль Уленшпигель" (1890) (партия первой скрипки); первой части скрипичного концерта Берга (1935) и струнного трио Веберна (1927) (партия скрипки). Одного взгляда на рисунок достаточно для того, чтобы понять: первые два произведения — Бетховена и Р. Штрауса, при всем их различии, принадлежат к одному типу музыки, а два последних — Берга и Веберна — к совершенно другому типу (хотя они также отличаются, между собой). Знатоки музыки воспримут этот факт как должное: ведь по отношению к Бетховену и Р. Штраусу Берг и Веберн — представители принципиально иного направления в музыке, так называемой додекафонной *или атональной музыки. Поскольку атональная музыка отрицает главную роль тоники и устойчивых звуков в ладу и считает все звуки равноправными, то и статистическое распределение высот звуков в атональной музыке должно быть более гладким по сравнению с тональной музыкой, где одни звуки являются явно предпочтительными (пики на полигоне относительных частот), а другие употребляются редко ("провалы" на полигоне).

*( Додекафония (от греч. dodeka — двенадцать и phone — звук) — метод музыкальной композиции, основанный на отрицании ладовых связей между звуками. В додекафонии все 12 звуков хроматической гаммы считаются абсолютно равными (откуда и происходит название) без различия устойчивых и неустойчивых звуков и без выделения тоники. Поэтому додекафонию называют также атональной музыкой. Метод додекафонии был разработан и внедрен австрийским композитором Арнольдом Шёнбергом (1874-1951). Альбан Берг (1885-1935) и Антон фон Веберн (1883- 1945) — ученики и последователи Шёнберга. )

Итак, тот факт, что Берг и Веберн — представители одного направления в музыке, а Бетховен и Р. Штраус — другого, нашел яркое выражение в статистических распределениях высот звуков у этих композиторов. Заметим, что Берг и Веберн, будучи пылкими последователями Шёнберга, сочиняли свою музыку по сходным и весьма строгим формальным правилам. Поэтому их статистические распределения так похожи, хотяу с другой стороны, и различаются тонкими деталями, которые характеризуют индивидуальные черты каждого композитора. Таким образом, уже простая статистика высот звуков позволяет выявить, с одной стороны, принадлежность автора к тому или иному направлению в музыке, а с другой — увидеть тонкие черты различия, характерные для конкретных произведений и конкретных композиторов. Однако пока мы ограничивались лишь качественными выводами. Посмотрим, нельзя ли извлечь из статистических распределений какие-либо количественные характеристики.