Александр Волошинов - Математика и искусство

Всякое статистическое распределение (x i, W i) i = l, 2, ..., k обладает двумя важнейшими числовыми характеристиками: эмпирической средней и эмпирической дисперсией. Эмпирической средней 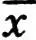называется среднее арифметическое значений х i, статистического распределения с учетом их частот п" т. е.

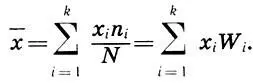(12.5)

Эмпирическая средняя характеризует "среднюю величину" значений статистического распределения. Однако помимо "средней величины" важно знать, насколько "разбросаны" значения ж, относительно этой средней величины, т. е. какова дисперсия (от лат. dispersus — рассыпанный) статистического рарпределения. Назовем разность x i— 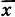отклонением значения x iот эмпирической средней 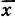. Легко видеть, что сумма всех отклонений с учетом их частот n i, равна нулю:

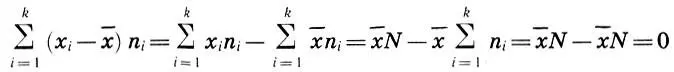
и, значит, не может быть взята в качестве характеристики рассеяния параметров статистического распределения. Поэтому в качестве характеристики разброса параметров x iберут среднее арифметическое квадратов отклонений. Итак, эмпирической дисперсией D называется среднее арифметическое квадратов отклонений значений х i, от их эмпирической средней 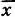с учетом частот n i, т. е.

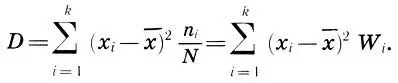(12.6)

Для вычисления эмпирической дисперсии существует также более практичная формула

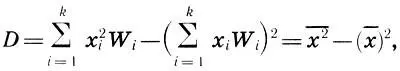(12.7)

т. е. эмпирическая дисперсия равна эмпирическому среднему квадратов значений статистического распределения минус квадрат эмпирической средней. Наконец, чтобы характеристики рассеяния имели ту же размерность, что и значения x iстатистического распределения, вместо дисперсии рассматривают среднее квадратическое отклонение

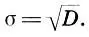(12.8)

Среднее квадратическое отклонение показывает, насколько узко или насколько широко распределены вокруг эмпирического среднего 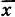значения статистического распределения x i.

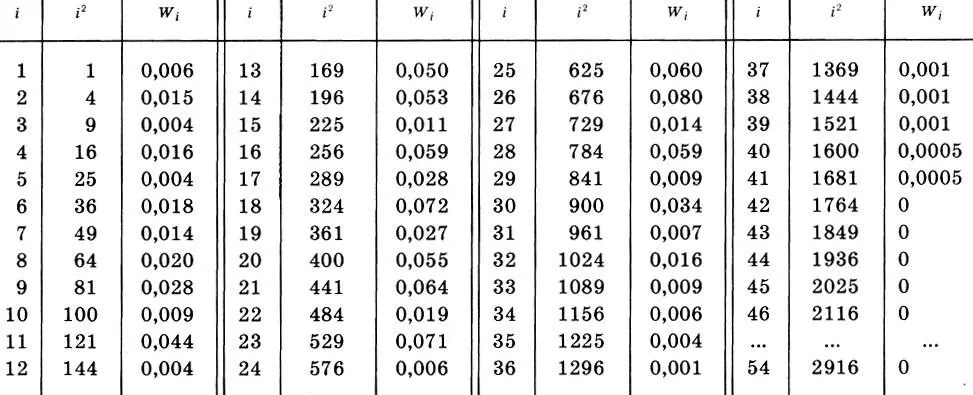
Таблица 3. Статистическое распределение (x i= i, W i) высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена. Для расчета дисперсии приведены также значения x i 2= i 2

В качестве примера найдем эмпирическую среднюю, эмпирическую дисперсию и среднее квадратическое отклонение для статистического распределения высоты звуков партии первой скрипки струнного квартета ми-бемоль мажор Бетховена (см. с. 168). Выпишем значения x i= i, x i 2= i 2и W i(i=l, 2, ..., 54) в виде таблицы 3. Легко проверить, что

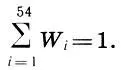
Подставляя данные таблицы 3 в формулы (12.6), (12.7) и (12.8), находим

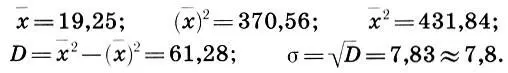
Итак, для струнного квартета Бетховена эмпирическая средняя 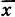= 19,25, т. е. "средним" звуком произведения является ре-бемоль второй октавы. Это еще мало о чем говорит. Вторая характеристика — среднее квадратическое отклонение — означает, что средний разброс звуков в произведении относительно ре-бемоль составляет ± 8 звуков, т. е. наиболее употребимые звуки произведения находятся в диапазоне 11≤i≤27, или от фа 1 до ля 2 . Среднее квадратическое отклонение высоты звуков музыкального произведения оказалось чрезвычайно эффективной характеристикой, позволяющей найти общие закономерности в развитии всей музыки. Остановимся на этом подробнее.

Как уже отмечали, основной целью работ Фукса было не просто найти какие-либо числовые характеристики произведений искусства, а выявить на основании этих характеристик закономерности общего порядка. С этой целью Фуксом были составлены статистические распределения высоты звуков в партиях первой скрипки большого числа произведений за период почти в пятьсот лет. Были определены числовые характеристики этих распределений, и прежде всего среднее квадратическое отклонение. Анализ поведения среднего квадратического отклонения дал блестящий результат: среднее квадратическое отклонение за последние 500 лет истории европейской музыки монотонно возрастает. Это уже есть не что иное, как закон развития музыки!

В таблице 4 приведены результаты исследований Фукса. Здесь представлены произведения, написанные с 1530 г. по 1960 г. Для каждого произведения было составлено статистическое распределение высоты звуков в партии первой скрипки, аналогичное таблице 3. Затем были определены средние квадратические отклонения в этих распределениях (найденное нами значение σ = 7,8 для струнного квартета ми-бемоль мажор Бетховена находится в соответствующем месте таблицы 4). Наконец, для каждого периода в истории развития музыки было вычислено среднее арифметическое о средних квадратических отклонений отдельных произведений. Разбиение на периоды проведено в соответствии с существовавшими в музыке направлениями. Так, в таблице 4 полифония строгого стиля представлена произведениями Вилларта, Модены, Палестрины, Хаслера, Шейна и Розенмюллера; полифония свободного стиля (барокко) — произведениями Коре л ли, Вивальди и Баха; классицизм — произведениями Моцарта, Бетховена и Шпора; романтизм — произведениями Шуберта, Шумана, Брамса, Р. Штрауса и Чайковского; неоромантизм — произведениями Хиндемита, Бартока и Эгка; додекафония — произведениями Шёнберга, Веберна, Берга и Ноно. Поэтому естественно, что одни периоды в таблице 4 далеко отстоят друг от друга, а другие — пересекаются. Достаточно одного взгляда на первый и последний столбцы таблицы 4, чтобы увидеть закономерность: за прошедшие 500 лет значение 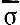возросло от 3,7 до 10,8, т. е. по мере развития музыки значение σвозрастает.