Александр Волошинов - Математика и искусство

Разумеется, математические методы в искусствознании применяются не для того, чтобы алгеброй вытеснить гармонию, а чтобы подтвердить интуицию художника, полнее раскрыть замысел гения, а быть может, и найти закономерности, отличающие совершенное произведение или хотя бы эпоху, в которую оно создано. Как говорил Пуанкаре, "Математика — это искусство называть разные вещи одним и тем же именем". Поэтому проникновение математических методов в анализ произведений искусства, безусловно, поможет назвать одним именем пока непонятные и несвязанные между собой законы искусства.

К сожалению для исследователя и к счастью для художника, законы искусства не столь прямолинейны и однозначны, как законы науки или языка. Эта "нелинейность" законов искусства и создает неимоверные трудности на пути исследователя искусства, но в то же время является источником все новых открытий в творчестве художника. Более того, искусство парадоксально и его парадоксальность не в состоянии выразить строгое логическое мышление. Вот только два примера из живописи. Какими законами механики описать движение саней, в которых едет суриковская боярыня Морозова? Уже сто лет, как бегут ее сани, бегут, оставаясь все время на одном месте... "Джоконда" Леонардо да Винчи и "Неизвестная" Крамского явно глядят на кого-то. Смотрят пристально, грустно и чуть усмехаясь, надменно и страдальчески, но смотрят на того, кого нет. Кипы статей написаны о том, на кого и как они смотрят, но все безрезультатно. Математика также бессильна перед чарами этих двух загадочных женщин.

Но у математики непочатый край проблем и в тех областях искусства, которые поддаются законам логики. Ведь математика делает только первые шаги в анализе искусства, которые сродни первым шагам медицины, начавшей изучение живого организма человека с познания законов его анатомического строения. Хорошо сказал об этом русский советский музыковед Э. К. Розенов (1861 — 1935): "Хотя, обнаруживая в живом творчестве и в созданном им живом художественном организме его сокрытый от взора внутренний механизм, притом, конечно, не весь, а одну какую-нибудь из двигающих его пружин, мы не дальше продвинемся по пути к проникновению в жизненные тайны, чем это делает анатомия, обнажающая скелет, мускулы и нервы живого организма, тем не менее мы не должны считать такие исследования бесцельными".

В начале нашего столетия на одном из заседаний Московского научно-музыкального кружка, членами которого вместе с композиторами и пианистами Танеевым, Рахманиновым, Глиэром, Гольденвейзером были и крупные московские ученые, Розенов выступил с докладом "Закон золотого сечения в поэзии и музыке". Эту работу можно считать одним из первых математических исследований музыкальных произведений. Остановимся на ней подробнее.

Очевидно, что при делении целого на две неравные части возможно бесконечное множество отношений между целым и одной из его частей, а также между самими частями целого. Но только в единственном случае эти отношения могут быть равными. Этот случай, как мы знаем (с. 79), и представляет собой золотое сечение, когда целое относится к большей части, как большая часть к меньшей.

Обозначая целое через а, большую часть х и, следовательно, меньшую а — х, имеем

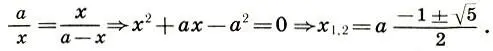(12.1)

Поскольку х есть часть целого, т. е. величина положительная, а второй корень (12.1) отрицателен, то приходим к единственному значению корня:

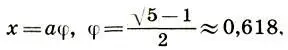(12.2)

где величина φ является коэффициентом золотого сечения. Тогда

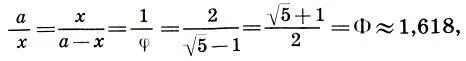(12.3)

причем Ф = 1/φ

Для меньшей части имеем а — х = а(1 — φ) = аφ 2, причем аφ + φ 2= а. Разделив теперь величину аφ в золотой пропорции, получим

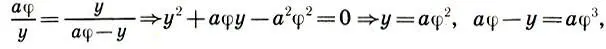
причем аφ 2+ аφ 3= аφ. Легко видеть, что большая часть второй золотой пропорции у = аφ 2совпадает с меньшей частью первой а — х = аφ 2. Итак, при последовательном делении целого а в золотой пропорции имеет место геометрическая прогрессия (ряд золотого сечения) со знаменателем φ, каждый член которой равен сумме двух последующих членов прогрессии:

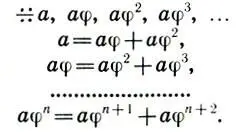(12.4)

Огромная роль золотого сечения в пространственных искусствах (скульптуре, архитектуре, живописи) известна с античных времен и имеет немало объяснений. Например, такое: линия глаз, на которой человек привык концентрировать свое внимание, слушая собеседника, делит длину лица в отношении золотого сечения. Поэтому при взгляде на любой предмет мы невольно направляем глаза в точку золотого деления, которая кажется нам привычной, естественной, а потому и красивой. Что касается искусств, развивающихся во времени (поэзия, музыка), то здесь неизвестны аналогичные природные предпосылки закона золотого сечения. Но тем более удивительным оказывается действие этого закона в поэзии и музыке, которое, по-видимому, первым обнаружил Розенов.

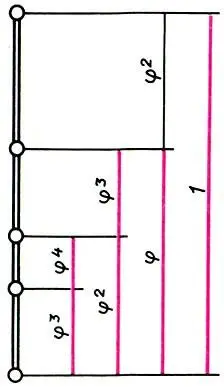
Последовательное деление единичного отрезка в золотом сечении

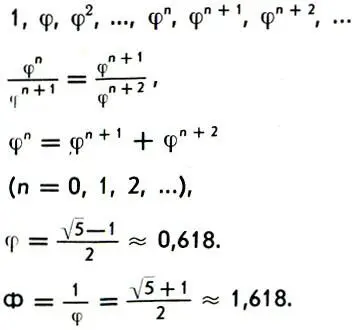
Ряд золотого сечения

Розенов проанализировал "популярнейшие и наиболее излюбленные произведения гениальных авторов Баха, Моцарта, Бетховена, Шопена, Вагнера, Глинки, а также произведения народного творчества наиболее древнего происхождения, живучесть которых является достаточным доказательством их эстетической ценности и широкой популярности". Остановимся на анализе Хроматической фантазии и фуги И. С. Баха, которые объединены общей тональностью ре минор и контрастны по жанру и образу. Хроматическая фантазия с фугой ре минор - одно из величайших творений Баха, образец совершенства формы и содержания, "могущественнейшее клавесинное произведение" (А. Н. Серов).

Хроматическая фантазия написана в размере 4/4, имеет 79 тактов, т. е. 79*4 = 316 четвертных долей. Итак, "целое" а = 316. Фантазия состоит из двух ясно различимых по характеру частей, отделенных друг от друга паузой. Первая часть, прелюдия, заканчивается на арпеджированном доминантовом трезвучии с разрешением на 2-й четверти 49-го такта, на которой стоит знак ферматы (удлинение звука), и затем идет пауза. Таким образом, первая часть фактически заканчивается на 3-й четверти 49-го такта, т. е. на 195-й (48*4 + 3) четверти (а 1=195). Вторая часть, пишет Розенов, "состоит из ряда в высшей степени выразительных колорированных речитативов, то развивающихся по силе, энергии и размаху До гигантской мощи, то нежных и жалобных, то сердитых и запальчивых, то впадающих в необычную для той эпохи романтическую мечтательность". На вторую часть приходится 121 четверть (а 2= а-а 1= 316 — 195 = 121). Вычисляя "теоретическую" длину первой части с помощью коэффициента золотого сечения, мы с поражающей точностью находим а 1= аφ = 0,316-0,618 = 195,3! Итак, Хроматическая фантазия разделена на первую и вторую части в золотой пропорции :