Александр Волошинов - Математика и искусство

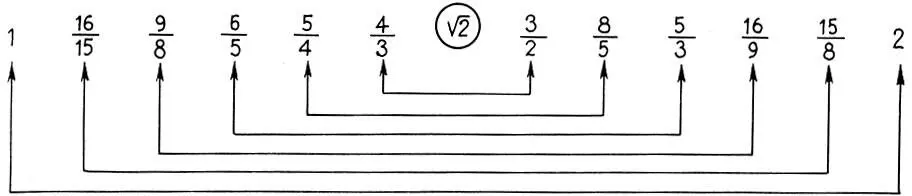
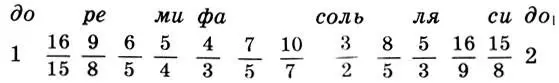(11.10)

Заметим, что, как и в диатонической гамме (11.9), интервальные коэффициенты хроматической гаммы (11.10) не содержат 11-й и 13-й обертоны, а печально известный "фальшивый" 7-й обертон входит только в два коэффициента (7/5 = 1,4 и 10/7≈1,428), которые приближенно равны интервальному коэффициенту тритона 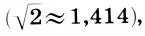чья дурная слава известна в музыке не менее.

Взяв, как и в (11.8), в качестве энгармонически равного звука для соль-бемоль (7/5) и фа-диез (10/7) их среднее геометрическое 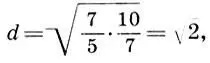, мы придем к 12-ступенной хроматической гамме чистого строя интервальные коэффициенты которой имеют вид

(11.11)

На этот раз интервальные коэффициенты в (11.11) не образуют никаких прогрессий. Однако, нетрудно обнаружить, что гамма (11.11) также обладает глобальной геометрической симметрией относительно 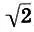, т. е.

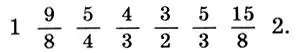
Гаммы (11.8) и (11.11) не обладают локальной геометрической симметрией, поэтому не допускают сдвигов без искажений. Последнее означает, что модуляции в другие тональности в пифагоровом и чистом строе затруднены.

Подведем некоторые итоги. Прежде всего мы видим, что музыкальные гаммы представляют собой строго упорядоченную совокупность звуков, отобранную из всего многообразия звуков, которые способно воспринимать и различать человеческое ухо. Именно закономерное построение гаммы, а следовательно и лада, позволяет на ее основе составлять и более сложные музыкальные конструкции, также носящие закономерный характер и называемые мелодией. Можно сказать, что гамма есть основная мелодия лада.

Отметим еще одно важное обстоятельство. В каждой из рассмотренных нами хроматических гамм: равномерно-темперированной (11.1), пифагоровой (11.8) и чистого строя (11.11) — точно выполнен один тип симметрии и только приблизительно другой. Так, равномерно-темперированная гамма (11.1) обладает локальной и глобальной геометрической симметрией, но в ней только приблизительно соблюдены пропорции деления октавы на квинту и кварту, большую и малую терции и т. д. Пифагорова гамма и гамма чистого строя обладают глобальной геометрической симметрией, но локальная симметрия в них выполнена только приблизительно. Зато в обеих гаммах точно соблюдено условие пропорционального деления октавы на квинту и кварту, а гамма чистого строя обладает еще двумя парами пропорций деления, что, видимо, и делает ее наиболее мелодичной из всех трех типов гамм.

Таким образом, в строении гаммы наряду с точной симметрией мы находим и приблизительную симметрию. (О загадках приблизительной симметрии и ее роли в науке и искусстве мы уже вели речь в главе 4.) Следовательно, в законах построения музыкальной гаммы отражается противоборство симметрии и асимметрии, олицетворяющих покой и движение, закономерное и случайное, вечное и сиюминутное. Именно диалектическое единство двух противоположных начал — симметрии и асимметрии — наполняет гамму подлинной гармонией, является источником вечной красоты и юного изящества музыкальной гаммы.

Последние три десятилетия поисками математических закономерностей в музыке усиленно занимается московский композитор М. А. Марутаев. Еще в студенческие годы М. Марутаева занимала мысль найти объяснение принципам музыкальной формы и ладогармонического языка. Результаты многолетних изысканий М. Марутаева легли в основу развитой им теории качественной симметрии чисел, позволившей автору определить меру нарушения симметрии в музыкальной гамме.

На основании теории качественной симметрии чисел Марутаев строит концепцию "универсальной гармонии", т. е., проще говоря, пытается решить одну из вечных загадок: найти "формулу красоты", "универсальную гармонию", которую искали еще древние греки и которая связала бы воедино законы природы и законы искусства.

К сожалению, и на сегодня это фантастическая задача, ибо человечеству пока не известны ни единые законы природы, ни тем более законы искусства.

Вот почему у концепции Марутаева много как пылких сторонников, так и ярых противников. Мы не будем останавливаться на концепции Марутаева, которая во многом спорна, а местами и просто содержит математические огрехи (но у кого хватит смелости объявить себя специалистом и в науке, и в искусстве?!), а отметим лишь некоторые любопытные факты, установленные Марутаевым.

Вновь обратимся к гаммам. Прежде всего заметим, что, хотя мы все время говорили о 12-ступенных хроматических гаммах, мы везде фактически включали в рассмотрение 13-ю ступень (октавное повторение основного тона), которая на самом деле является 1-й ступенью следующей октавы. Если в гаммах (11.1), (11.8) и (11.11) октавное повторение основного тона не рассматривать, то получается действительно 12-ступенные музыкальные ряды, которые Марутаев называет качественными музыкальными рядами , поскольку они состоят из оригинальных качеств:

1,37

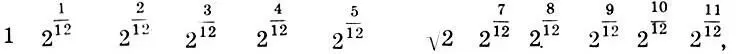(1.12)

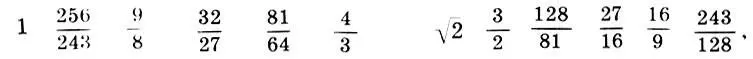(1.13)

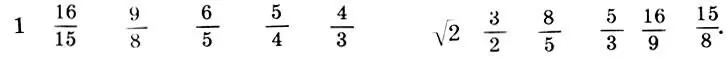(1.14)

Легко видеть, что качественная равномерно-темперированная гамма (11.12) сохраняет свойство глобальной геометрической симметрии, центр которой сместился из точки 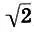≈1,41 в точку 2 11/24≈1,37:

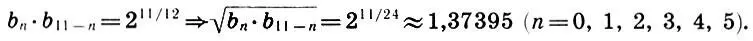
А вот для качественных гамм пифагорова и чистого строя глобальная геометрическая симметрия нарушится и будет выполняться только приблизительно. В самом деле, вычисляя среднее геометрическое для равноудаленных от концов членов ряда (11.13)