Александр Волошинов - Математика и искусство

Если прологарифмировать (11.1) — (11.3) по основанию 2, то эти соотношения примут наиболее простой вид

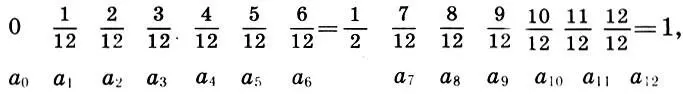(11.4)

(11.5)

(11.6)

Здесь a k= log 2b k(k = 0, l, 2, ..., 12). Равенства (11.4) — (11.6) выражают тот простой факт, что логарифмическая октава [0; 1] разбита на 12 равных частей. Поэтому каждые три соседних члена (11.4) симметричны относительно среднего из них и отстоят от него на расстояние 1/12 (локальная симметрия), а середина логарифмической октавы а 6=1/2 является центром ее глобальной симметрии, т. е. для каждого а nслева от а 6существует симметричный относительно а 6член a 12-nсправа от а 6, так что расстояния a 12-n— а 6и а 6— а nравны (n = 0, 1, 2, ..., 5).

Из равенств (11.1-3) или (11.4-6) очевидно, что при любых сдвигах (геометрических для (11.1) или арифметических для (11.4) структура равномерно-темперированной гаммы не нарушается, т. е. равномерно-темперированная гамма допускает модуляции в любые тональности. Эти возможности равномерной темперации, как отмечалось в главе 9, блестяще проиллюстрировал И. С. Бах в своем "Хорошо темперированном клавире".

Рассмотрим теперь лидийскую гамму пифагорова строя, или натуральный мажор (8.1), взяв в качестве дополнительных ступеней пониженные звуки ( ре-бемоль, ми-бемоль, соль-бемоль, ля-бемоль, си-бемоль ) и один повышенный звук ( фа-диез ) согласно (8.2):

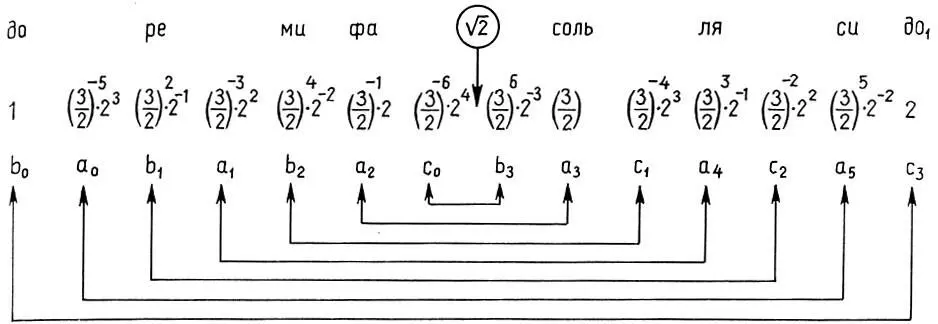(11.7)

Структура пифагоровой гаммы (11.7) значительно сложнее. Однако при ближайшем рассмотрении можно обнаружить, что пифагорова гамма состоит из трех геометрических прогрессий, переплетенных между собой, подобно Платонову гептахорду (7.1), причем все три прогрессии имеют одинаковый знаменатель :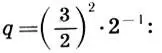

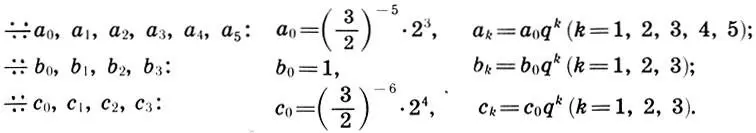
Для этих прогрессий справедливы соотношения

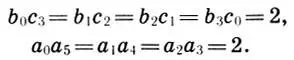
Учитывая расположение членов прогрессии в (11.7), приходим к выводу, что пифагорова гамма, также обладает глобальной геометрической симметрией. Следовательно, 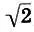является центром глобальной симметрии пифагоровой гаммы.

Но 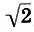не является ступенью гаммы (11.7). Кроме того, в (11.7) осталась одна пара энгармонически неравных звуков соль-бемоль и фа-диез . Если в качестве энгармонически равного звука для соль-бемоль 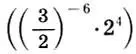и фа-диез 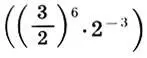взять их среднее геометрическое 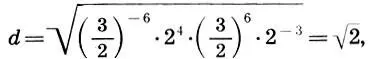, то оно оказывается в точности равным центру глобальной симметрии 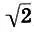. Таким образом, мы получим 12-ступенную хроматическую пифагорову гамму с центром глобальной симметрии 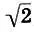на седьмой ступени:

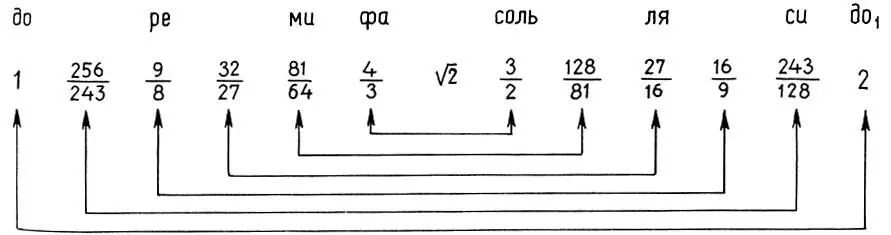(11.8)

Легко проверить, что в гамме (11.8) можно взять чистые квинты на всех ступенях, кроме седьмой ( 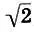), которая даст "волчью" квинту. Кроме того, сам интервал тритона ( 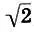), как мы знаем, является резким диссонансом. Оба этих качества составили тритону печальную славу. В средние века тритон называли "дьяволом в музыке", и до XVI века употреблять его в церковных песнопениях строго запрещалось.

Рассмотрим теперь диатоническую 7-ступенную гамму чистого строя (8.7):

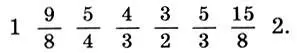(11.9)

Мы знаем, что гамма чистого строя является наиболее благозвучной, а ее интервальные коэффициенты имеют самый простой вид. Но еще удивительнее то, что гамма (11.9) является и самой пропорциональной. В самом деле, среднее арифметическое и среднее гармоническое основного тона (1) и октавы (2) дают нам квинту и кварту:

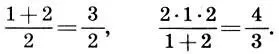
Среднее арифметическое и среднее гармоническое основного тона и квинты образуют большую и малую терции:

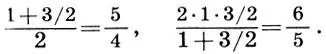
Наконец, взяв среднее арифметическое и среднее гармоническое основного тона и большой терции, мы получим оба интервала тона чистого строя:

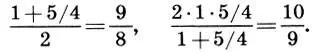
Таким образом, все главные интервалы чистого строя получаются как последовательная цепь средних пропорциональных, началом которой является пропорциональное деление октавы на квинту и кварту.

Перейдем к хроматической гамме чистого строя. Для построения дополнительных ступеней хроматической гаммы отложим полутон чистого строя (16/15) вверх от 1, 2, 4, 5 и 6-й ступеней диатонической гаммы (11.9), т. е. умножим их интервальные коэффициенты на 16/15, а также из соображений симметрии отложим полутон вниз от 5-й ступени. В результате получим 13-ступенную гамму:

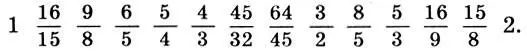
Интервальные коэффициенты 45/32 и 64/45 можно заменить на более простые 7/5 и 10/7, которые приближенно им равны 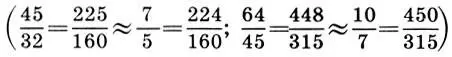и также обладают геометрической симметрией относительно 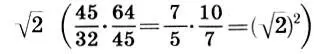. В результате входящие в хроматическую гамму чистого строя интервальные коэффициенты выразятся с помощью отношения натуральных чисел, не превосходящих 16, которые можно трактовать как частоты первых 16 гармоник основного тона (1), или первые 16 ступеней натурального звукоряда: