Александр Волошинов - Математика и искусство

Таким образом, мы выполнили обещание, данное на с. 130 и объяснили, почему пифагорова терция в гармоническом исполнении звучит напряженно по сравнению с чистой. Конечно, теория Гельмгольца не решает всех музыкальных загадок колеблющейся струны — таких как проблема 7-го обертона, например,- и здесь еще остается немало точек приложения для пытливого ума.

Не правда ли, какое удивительное разнообразие законов, свойств и загадок таит в себе простое колебание простой струны! Законы Пифагора — Архита (особенно "закон консонансов"), законы Мерсенна и законы Юнга, решения Д'Аламбера Д. Бернулли и Фурье, натуральный звукоряд и мажорное трезвучие, биения... Вот уже третье тысячелетие обыкновенная струна открывает человечеству свои необыкновенные тайны! И быть может, кто-то задумается следующий раз об этих тайнах, прежде чем ударить по струнам старенькой гитары.

Если окинуть взглядом 2500 лет истории европейской музыки, от Пифагора и до наших дней, то слова П. И. Чайковского, вынесенные в эпиграф, обретают особый смысл. В самом деле, каких только переворотов в мировоззрении, сознании и бытии человечества не произошло за это время! Но основа музыки — музыкальная гамма — остается практически неизменной. Музыкальная гамма даже в наш бурный век представляется незыблемым утесом в клокочущем море новых идей и теорий.

Но в чем причина такого завидного долголетия музыкальной гаммы? Почему из всего обилия звуков с частотой от 16 до 20000 Гц, которые способно воспринимать наше ухо (в области до 4000 Гц мы отличаем звуки, отстоящие друг от друга по

частоте всего на одно колебание в секунду, т. е. почти 4000 звуков!), в музыке используется всего 7 октав по 12 звуков, т. е. всего 84 звука [22] Для педантов уточним, что концертный рояль имеет до 90 клавиш (звуков). ?

Объяснить, почему музыкальный звукоряд содержит именно 7 октав, нетрудно. В самом деле, возьмем самую нижнюю ноту звукоряда — ля — субконтроктавы, частота которой равна 27,5 Гц, т. е. находится у нижней границы слышимости звуков. (Подходить ближе к границе слышимости не стоит, так как у каждого человека она своя и, значит, некоторые люди не услышат более низкие звуки.) Рассмотрим 8 октавных повторений этой ноты:

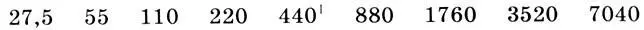
*( Частота ноты ля первой октавы — 440 Гц — является эталонной при настройке фортепиано и проверяется по камертону. Относительно этой ноты сохранилось интересное предание: в Древнем Египте около города Фивы находилась огромная статуя эфиопского Царя Мемнона. Статуя была повреждена во время землетрясения и каждое утро на рассвете якобы издавала звук ля,, который считался голосом Мемнона. Фивские музыканты приходили к статуе настраивать свои инструменты. К сожалению, в начале нашей эры голос Мемнона звучать перестал и проверить правоту предания невозможно. )

Легко видеть, что восьмая октава выходит далеко за границу четкой различимости высоких звуков (4000 Гц), и, таким образом, в диапазоне до 4000 Гц укладывается чуть более 7 октав. Выходить же за границу 4000 Гц нет смысла, так как звуки там плохо различаются по высоте и мелодия будет теряться.

Итак, в диапазоне от 16 до 4000 Гц укладывается чуть более 7 октав. Октав-ные звуки воспринимаются как подобные, родственные (это объясняется, как мы уже знаем, совпадением большого числа их гармоник) и служат своего рода масштабными метками в музыкальной шкале. Следовательно, построение музыкальной шкалы сводится к искусному делению октавы на составные части.

Почему октава разделена именно на 12 частей, мы уже объяснили в предыдущей главе. Как показала история развития музыки, только при таком делении октавы достигается та "строгая соразмеренная гармония всех частей, объединяемых тем, чему они принадлежат,- такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже". Эти слова, как мы знаем (с. 17), являются определением красоты по Альберти. Красота же вечна. Таким образом, именно в пропорциональном гармоничном делении октавы на составные части и заключается источник красоты музыкальной гаммы, а значит, и секрет ее трехтысячелетнего долголетия.

Мы уже отмечали некоторые пропорции музыкальной гаммы. Мы также знаем, что пропорциональность и симметрия являются объективными признаками красоты. Однако чем ближе всматриваешься в музыкальную гамму, тем полнее раскрываются все новые закономерности ее пропорционального строения, а значит, и объективные законы ее красоты. Остановимся подробнее на некоторых из этих закономерностей.

Рассмотрим вначале равномерно-темперированную 12-ступенную хроматическую гамму (9.1), имеющую наиболее простое строение:

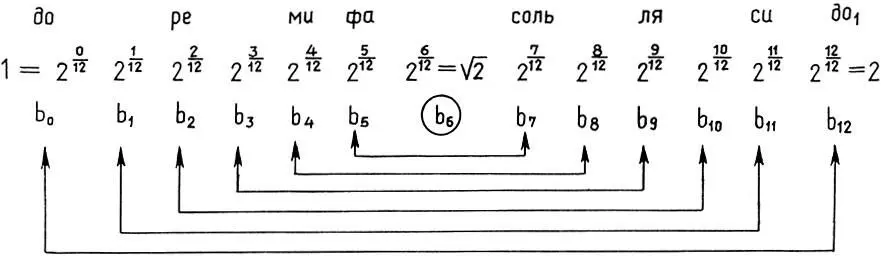(11.1)

Легко видеть, что ступени равномерно-темперированной гаммы (11.1) образуют геометрическую прогрессию со знаменателем 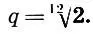. Тогда

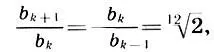или 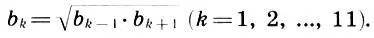(11.2)

Следовательно, каждая внутренняя ступень гаммы (11.1) является средним геометрическим своих соседей. Назовем это локальной геометрической симметрией с коэффициентом симметрии (отношением входящих в пропорцию членов) .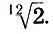

Кроме того, гамма (11.1) обладает глобальной геометрической симметрией, т. е. произведения членов (11.1), равноудаленных от концов, равны квадрату среднего члена b 6:

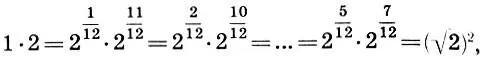
или 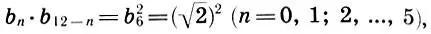откуда имеем

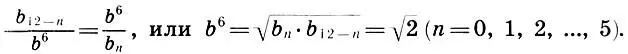(11.3)

Таким образом, седьмая ступень (11.1) b 6= 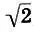, так называемый тритон , равный увеличенной кварте или уменьшенной квинте, является средним геометрическим любой пары равноудаленных от концов ступеней. Назовем тритон b 6= 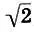, центром глобальной геометрической симметрии гаммы (11.1). Глобальная геометрическая симметрия связывает интервал и его обращение через интервальный коэффициент октавы.