Александр Волошинов - Математика и искусство

Ну а минорное трезвучие? Споры о природе минора не затихают и по сей день. В них участвовали Рамо, Д'Аламбер, Руссо, Гёте, Гельмгольц, многие наши современники. На сегодня мнения сходятся в том, что поскольку в минорном трезвучии (до — ми-бемоль — соль) второй звук (ми-бемоль) лежит на полутон ниже пятой гармоники основного тона, то он образует с ней едва слышимый диссонанс, который и обусловливает некоторую "затененность", "нечто мрачное и неясное, необъяснимое для слушателя" (Гельмгольц). По o этой причине в музыке Баха, Генделя, Моцарта минорные произведения часто заканчиваются мажорным — наиболее натуральным, просветленным — аккордом.

Итак, в мажорной гамме третья ступень как бы тяготеет вверх, тогда как в минорной она тяготеет вниз. Движение же вверх воспринимается нами как восхождение к свету, просветление, радость. Напротив, движение вниз ассоциируется со спуском в темноту, затемнением, печалью. Эти объективные предпосылки поддерживаются, кроме того, определенной традицией применения мажора и минора. В тех же случаях, когда эти традиции нарушаются, мы встречаем разудалую песню "Яблочко", написанную в миноре, и молитву " Ave Maria ", которую, несмотря на ее название — "Радуйся, Мария" — и мажорный лад, никак не назовешь веселой. К сожалению, смешивание объективных физико-математических законов строения мажора и минора с их субъективной эстетической оценкой породило вокруг них много ненужных споров.

В заключение остановимся еще на одной проблеме колеблющейся струны. До сих пор, следуя решению (10.9), мы пытались "разъять, как труп" колебания струны на простейшие гармонические составляющие. Но ведь на самом деле, опять же согласно (10.9), составляющие колебание струны гармоники складываются, образуя сложную картину колебаний. Характер этой картины зависит прежде всего от амплитуд гармоник. Решить эту задачу в общем виде не просто, поэтому остановимся на более простой задаче.

Пусть складываются два колебания постоянной и одинаковой амплитуды, равной для простоты единице, и разных частот ω 1<���ω 2:

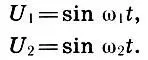
Суммарное колебание, пользуясь формулами суммы синусов и косинуса половинного угла, представим в виде

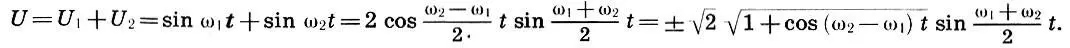(10.13)

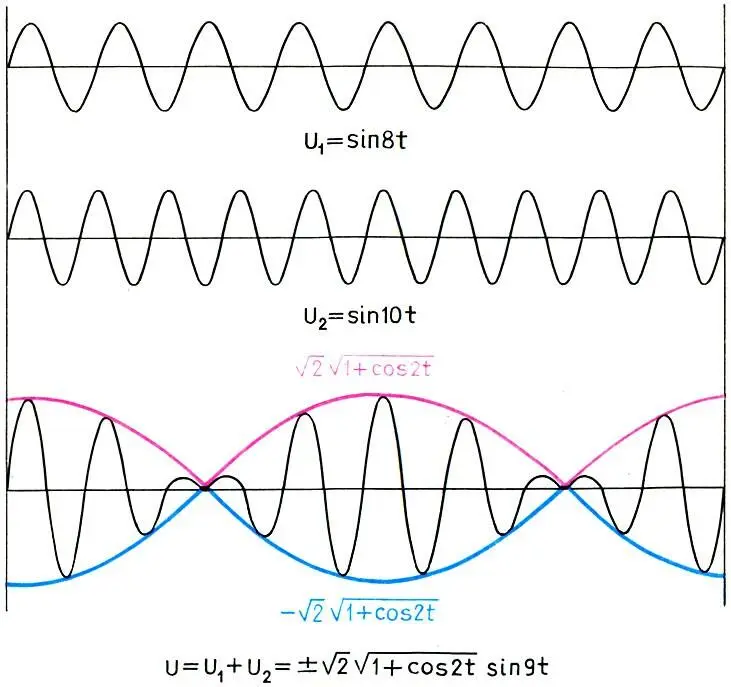
При сложении двух колебаний, близких по частоте (ω 1= 8 и ω 2= 10), возникают биения — периодическое усиление и ослабление звука, происходящее с частотой биений ω = ω 2— ω 1= 2

Равенство (10.13), когда частоты ω 1и ω 2близки друг к другу с достаточной степенью точности, можно трактовать следующим образом: сумма двух гармонических колебаний частот ω 1и ω 2является "почти гармоническим" колебанием, частота которого есть среднее арифметическое данных частот 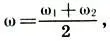, а амплитуда изменяется во времени с частотой ω 2-ω 1и ограничена сверху функцией , а снизу — функцией — 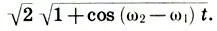. Легко видеть, что амплитуда суммарного колебания пульсирует с частотой ω 2-ω 1от нуля до максимального значения и затем снова до нуля. По этой причине такие колебания называют биениями . Из (10.13) также видно, что максимальная амплитуда биений вдвое больше амплитуд составляющих колебаний.

Итак, при сложении двух близких по частоте колебаний возникают биения" т. е. почти гармонические колебания с частотой, равной средней частоте данных колебаний, и амплитудой, пульсирующей с частотой биений, которая равна разности частот данных колебаний. Издаваемый при биениях звук то периодически усиливается, то замирает.

Перейдем к музыкальной стороне явления биений. Известно, что всякое прерывистое раздражение нервов воспринимается сильнее, чем постоянное. Однако с увеличением частоты раздражений нерв не успевает следить за изменениями, отдельные раздражения сливаются между собой и становятся незаметными. Экспериментально установлено, что наиболее отчетливо слышны биения с частотой 4-5 Гц (колебаний в секунду). Биения с частотой около 15 Гц еще различимы, а при частоте около 30 Гц они начинают сливаться, но создают неприятное ощущение хрипловатости звучания.

Существует теория Гельмгольца, которая объясняет явления консонанса и диссонанса биениями, возникающими между гармониками двух звучащих основных тонов. Согласно теории Гельмгольца, от наличия биений, их частоты и громкости (амплитуды) зависит степень консонантности и диссонантности интервала. Поясним эту теорию на примере. В таблице 2 в качестве основного тона взяты нота до малой октавы, частота которой равна 131 Гц, и ее пять обертонов. Далее приведены первые пять обертонов для звуков до 1, соль, фа, ми (чистого строя), ми (пифагорова строя) и до-диез (чистого строя), которые образуют с основным тоном до соответственно интервалы октавы, квинты, кварты, большой терции, пифагоровой терции и малой секунды.

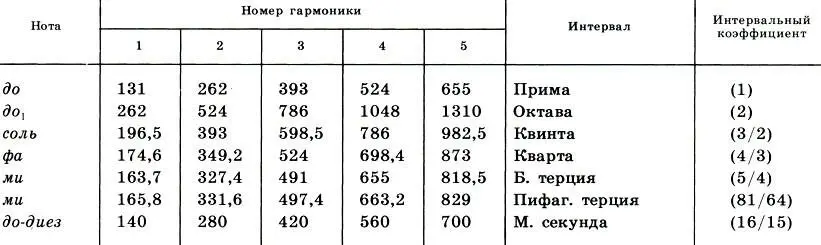
Таблица 2. Основные гармоники ноты до малой октавы и нот, образующих с до важнейшие интервалы

Понятно, что для октавы совпадают частоты гармоник, номера которых относятся как 2/1, для квинты — как 3/2 и т. д. (см. табл. 2). Сравнивая частоты первых гармоник, мы видим, что чем меньше становится интервал, тем ближе частоты основных тонов, тем различимее будут биения и, следовательно, тем меньше будет степень консонантности интервала. Поэтому самым консонантным интервалом является октава, затем идут квинта и кварта. Все три этих интервала не дают биений и относятся к совершенным консонансам. Терция дает в первых гармониках чуть более 30 биений, т. е. на пороге различимости, и поэтому относится к несовершенным консонансам. А вот малая секунда дает 9 биений (140-131 = 9) и поэтому является явным диссонансом. Заметим, что четвертая гармоника пифагоровой терции (663,2) и пятая гармоника основного тона (655) дают 8 биений (663-655 = 8). Эти биения и создают неприятное гармоническое звучание пифагоровой терции. Однако поскольку они происходят в старших гармониках, т. е. значительно слабее биений в первых гармониках, то ясно, что пифагорову терцию нельзя причислить к диссонансу наравне с малой секундой, где такие же биения происходят в первых гармониках.