Джо Боулер - Математическое мышление

Рис. 5.12.Максимальную площадь ограждает забор в виде правильного многоугольника с 36 сторонами

Ученики разделили свою фигуру на 36 треугольников; им было известно, что длина основания треугольника составляет 1 м, а угол при вершине — 10° (рис. 5.13).

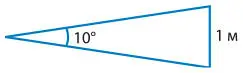
Рис. 5.13.Треугольник, образованный секцией забора длиной 1 м

Но этого было недостаточно, чтобы найти площадь треугольника. И тут учитель объяснил детям суть тригонометрии и способы использования функции тангенса для определения высоты треугольника. Ученики были в восторге: так кстати пришелся новый метод. Я видела, как один мальчик взахлеб объяснял членам своей группы функцию тангенса, оценивая новое знание как «действительно крутое». В этот момент я вспомнила об уроке совсем иного рода, за которым я наблюдала в обычной школе неделей ранее. Учитель объяснил ученикам тригонометрические функции и дал им целые страницы с упражнениями.

Ученики считали, что тригонометрические функции очень скучны и не имеют отношения к их жизни. В школе, придерживающейся проектно-ориентированного подхода, ученики с воодушевлением исследовали тригонометрию и считали эти методы интересными и полезными. В результате они глубже освоили методы. И именно поэтому ученики школы с таким подходом к преподаванию математики более успешны на экзаменах и в жизни.

Второй пример того, как ученики изучали методы после постановки задач, взят из исследования, которое я проводила в США. Оно также показало, что ученики добились гораздо лучших результатов, когда им преподавали математику на основе концептуального подхода, сфокусированного на связях и коммуникации (Boaler & Staples, 2005). Более подробная информация об обоих подходах к преподаванию представлена в моей книге «При чем тут математика?» (Boaler, 2015). Однажды я присутствовала на уроке по началам анализа в успешной школе, которую я назвала Рейлсайд. Урок был посвящен определению объема сложной фигуры. Лора Эванс готовила учеников к изучению анализа и поиску площади под кривой с помощью интегралов, но не стала с самого начала объяснять формальный метод, как обычно бывает. Она поставила задачу, для которой были нужны эти знания, и предложила детям подумать, как ее решить. Задача состояла в том, чтобы найти способ определения объема лимона. Чтобы ученики могли поразмышлять над этим, учительница дала каждой группе лимон и большой нож и предложила исследовать возможные решения (рис. 5.14).

Рис. 5.14.Чему равен объем лимона?

Источник: Shutterstock (ampFotoStudio).

После того как ученики обсудили эту задачу в группах, некоторые из них подошли к доске и с воодушевлением поделились своими идеями. Одна группа решила погрузить лимон в миску с водой, чтобы вычислить объем вытесненной жидкости. Вторая — тщательно измерить размер лимона. Третья — разрезать лимон на тонкие дольки и представить их себе в виде двумерных сечений, которые они затем разрезали на полоски, приблизившись к формальному методу определения площади под кривой, которому обучают в рамках курса математического анализа (рис. 5.15).

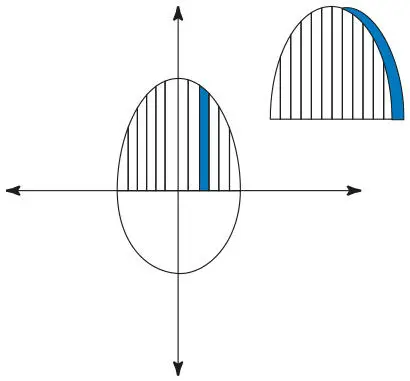
Рис. 5.15.Вычисление объема лимона по сечениям

Когда учительница объяснила детям метод интегралов, те с воодушевлением приняли его как эффективный инструмент.

В обоих случаях применялся обратный порядок обучения. Ученики узнали о тригонометрических методах и пределах после того, как исследовали задачу и столкнулись с необходимостью в конкретных приемах. Учителя объяснили эти методы в тот момент, когда в них возникла необходимость, вместо того чтобы сначала дать формальную информацию, а потом предложить отработать метод. Это пробудило у учеников огромный интерес к изучаемым методам и помогло понять их.

Как я упоминала в главе 4, Себастьян Трун поведал мне, насколько важную роль сыграла интуиция в его работе. Он сказал, что ему не удавалось продвинуться в решении задачи, если у него не было интуитивного ощущения, что он на верном пути. Математики также подчеркивают роль интуиции в их работе. Леоне Бертон провела опрос среди 70 математиков, занимающихся научными исследованиями, и 58 из них отметили этот факт (Burton, 1999). Рубен Херш пришел к тому же выводу: «Интуиция в математике повсюду» (Hersh, 1999). Так почему же ее не применяют на большинстве уроков математики? Многие дети даже не представляют себе, что интуиция нужна при решении задач. Когда ученикам предложили поразмышлять над определением объема лимона, их попросили прибегнуть к интуиции. С ее помощью можно решать многие математические задачи. Детям помладше стоит дать разные треугольники и прямоугольники и предложить подумать, как найти площадь треугольника, до того как объяснить им формулу площади. Ученики могут анализировать различия между наборами данных до того, как им объяснят такие понятия, как среднее арифметическое, мода и амплитуда. Они могут исследовать соотношения в окружностях, прежде чем узнают значение π. И когда эти ученики начнут изучать формальные методы, этот процесс будет более глубоким и содержательным. Мыслить интуитивно — очень полезное занятие. Во-первых, дети перестают пользоваться конкретными методами и анализируют задачи в более широком контексте. Во-вторых, они осознают, что должны использовать разум: мышление, осмысление и умозаключения. Они уже не думают, что их задача — простое воспроизведение методов, и понимают, что им нужно анализировать целесообразность применения разных подходов. В-третьих, как показали исследования Шварца и Брэнсфорда, мозг учеников настраивается на изучение новых методов (Schwartz & Bransford, 1998).

Следующий пример взят из семинара по профессиональному развитию, за которым я наблюдала. Мероприятие вела Рут Паркер — удивительный педагог, которая организует для учителей семинары, помогающие им понять математику на совершенно новом уровне. Я выбрала именно этот пример, поскольку в тот день увидела то, с чем сталкивалась впоследствии неоднократно: задачу, которая позволила учительнице по имени Элизабет увидеть настолько сильную математическую связь, что она расплакалась. Элизабет — учительница начальной школы, которая, как и многие другие, преподавала математику как набор процедур. Она не знала, что это наука, в которой есть много глубоких связей. Люди, которые всегда считали математику бессвязным набором процедур, нередко волнуются, когда видят глубокие связи в математике.