Джо Боулер - Математическое мышление

Как показано на рис. 5.3–5.10, люди представляют себе рост фигуры разными способами. Не предлагая ученикам мыслить визуально, мы упускаем прекрасную возможность помочь им лучше понять происходящее. Ниже показано, как учителя и ученики, с которыми я работала, представляют себе рост фигуры, и приведены названия, которые они использовали для обозначения своих вариантов.

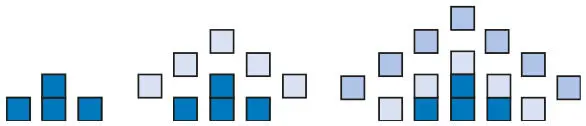
Рис. 5.3.Метод дождевых капель — кубики падают на столбцы с неба, как капли дождя

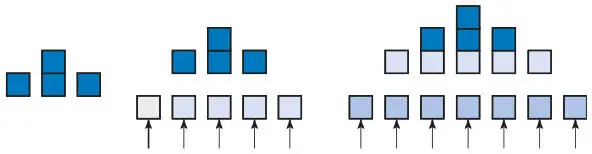
Рис. 5.4.Метод боулинга — кубики расставляются, как кегли на дорожке для боулинга

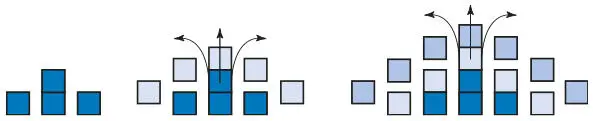
Рис. 5.5.Метод вулкана — средний столбец растет в высоту, а остальные растекаются, как лава из вулкана

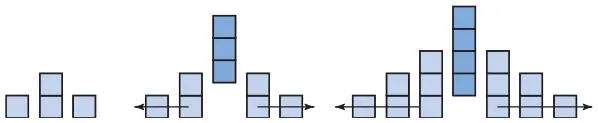
Рис. 5.6.Метод расхождения вод Красного моря — два столбца расходятся, и между ними появляется еще один

Рис. 5.7.Метод подобных треугольников — уровни можно рассматривать в виде треугольников

Рис. 5.8.Метод сечения — уровни можно рассматривать по диагонали

Рис. 5.9.«Лестница в небеса: в доступе отказано» — из фильма «Мир Уэйна»

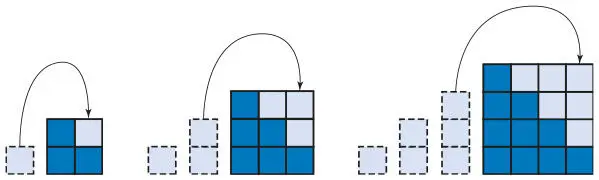
Рис. 5.10.Метод квадратов — любую фигуру можно перегруппировать, сделав из нее квадрат

Недавно я дала эту задачу на рост закономерности группе учителей старших классов, которые не стали тратить время на визуальное представление роста фигуры, составив вместо этого таблицу значений.

Когда я попросила учителей объяснить, почему эта функция возрастает по квадратичному закону, они не смогли ответить. Но мы видим здесь квадратичную функцию вот почему: фигура растет как квадрат со стороной ( n + 1), где n — номер шага (рис. 5.11).

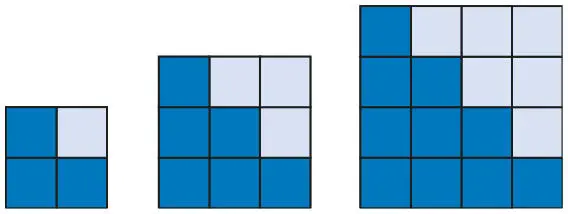
Рис. 5.11.Метод квадратов 2

Если мы не предлагаем ученикам проанализировать рост фигуры визуально, они не могут понять важные аспекты роста функции. Часто они не способны сказать, что означает n , и алгебра остается для них тайной: набором абстрактных символов, которые они переставляют на странице с места на место. Наши ученики летней школы знали, что представляет собой n , поскольку сами его нарисовали. Они знали, почему функция растет по квадратичному закону и почему n -й шаг представлен в виде ( n + 1) 2. Алгебраическое выражение, которое ученики в итоге составили, имело для них смысл. Кроме того, они не считали, что ищут стандартный ответ; они полагали, что исследуют разные методы и используют свои идеи, в том числе способы визуального представления математического роста. Ниже пойдет речь о том, как свойства данной задачи можно использовать в других задачах, чтобы повысить вовлеченность и понимание учеников.

Когда я рассказываю учителям об открытых, исследовательских задачах по математике, например задаче о росте фигур или «дождевых каплях», о которых шла речь выше, они часто спрашивают: «Я понимаю, что эти задачи увлекательны и рождают интересные математические дискуссии, но как ученикам осваивать новые концепции, например тригонометрические функции? Или как разлагать числа на множители? Они не могут открыть это для себя самостоятельно». Это обоснованный вопрос, и поиску ответа на него посвящен ряд важных исследований. Идеальные математические дискуссии — те, в ходе которых ученики используют математические методы и концепции для решения задач. Но иногда учителям нужно познакомить учеников с новыми методами. На большинстве уроков математики применяется стандартный подход: учителя объясняют методы, а ученики отрабатывают их, решая задачи из учебника. На уроках математики более высокого уровня ученики выходят за рамки отработки конкретных приемов и используют их для решения прикладных задач, но порядок сохраняется: учителя объясняют методы, а ученики применяют их.

В ходе одного важного исследования были сопоставлены три подхода к преподаванию математики (Schwartz & Bransford, 1998). Первый распространен в США: учитель объяснял методы, а ученики с их помощью решали задачи. При втором подходе ученики имели возможность открыть эти методы для себя в рамках исследований. Третий представлял собой обратный вариант типичной последовательности: ученикам сначала ставили прикладные задачи, над которыми они должны были работать, не зная, как их решить, а затем объясняли необходимые для этого методы. Именно третья группа учеников показала гораздо более высокие результаты. Исследователи обнаружили: когда ученикам предлагали решить задачи и они не знали методов, но им давалась возможность провести исследования, у них возникало любопытство и их мозг был настроен на изучение нового. И когда учителя объясняли эти методы, ученики уделяли им больше внимания и были более заинтересованы. Результаты исследования были опубликованы в статье под названием «Пора рассказать». По мнению исследователей, вопрос не в том, должны ли мы рассказывать о методах или объяснять их, а в том, когда это лучше делать. Результаты исследования однозначно указывают: самый подходящий момент наступает после того, как ученики исследуют задачу.

Как это происходит на уроке? Как учителям удается ставить ученикам задачи, которые они не могут решить, так чтобы те не испытывали разочарования? Чтобы объяснить, как это работает, приведу два разных примера такого подхода к преподаванию.

Первый взят из научного исследования, которое я проводила в Англии. Оно показало, что ученики, изучавшие математику на основе проектно-ориентированного подхода, добились гораздо более высоких результатов как при сдаче стандартных тестов (Boaler, 1998), так и позже (Boaler, 2005), по сравнению с теми, кто применял традиционный подход. В рамках одной из задач, о которой я узнала в школе, работающей на основе проектно-ориентированного подхода, группе тринадцатилетних учеников сказали, что фермеру нужно оградить забором как можно большую площадь 36 планками длиной 1 м. Ученики начали исследовать способы определения максимальной площади. Они пробовали квадраты, прямоугольники и треугольники, пытаясь найти фигуру с максимально возможной площадью. Два ученика поняли, что самую большую площадь имеет фигура, состоящая из 36 сторон, и приступили к определению ее точной площади (рис. 5.12).