Джо Боулер - Математическое мышление

Все наши уроки записывались на видео. Просматривая запись того, как эти мальчики работали в тот день, мы увидели, что они активно обсуждают числовые закономерности, визуальный рост и алгебраическое обобщение. Такая глубокая вовлеченность отчасти объяснялась тем, что мы использовали адаптированный вариант задачи. Адаптацию можно выполнять применительно к любым математическим заданиям. На уроках, когда ученикам дают задачи с функциями, обычно требуется определить значение на шаге 100 и в общем виде на шаге n . Мы начали не с этого, а с того, что попросили учеников самостоятельно поразмышлять о том, как они представляют себе рост фигуры, прежде чем переходить к групповой работе. Мы предложили им поразмышлять над этим на визуальном уровне, а не с помощью чисел, и нарисовать в своих тетрадях, где они представляют себе дополнительные кубики на каждом шаге. Мальчики по-разному увидели картину происходящего. Люк и Хорхе представили себе рост фигуры в виде прибавления кубиков к нижней части. Позже этот вариант получил в классе название «метод боулинга»: кубики расставляются, как кегли на дорожке. Карлос представил себе рост фигуры в виде кубиков, которые устанавливаются на верхушки столбцов. Этот подход стал известен как «метод дождевых капель» — кубики падают на столбцы сверху, как капли дождя с неба (рис. 5.2).

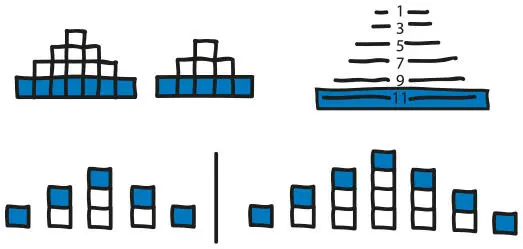
Рис. 5.2.Работа учеников

Источник: Selling, 2015.

Поработав над задачей о росте функции индивидуально, ученики обсудили, кто как представляет себе дополнительные кубики на каждом шаге. Поразительно, что они связали свои визуальные методы с количеством кубиков в каждой фигуре; и не только работали со своими методами, но и находили время объяснить их друг другу и применить методы друг друга. Рост функции заинтриговал этих троих мальчиков, и они настойчиво пытались определить значение на шаге 100, вооружившись своими знаниями о визуальном росте фигуры. Мальчики предлагали друг другу идеи, наклонившись над столом и показывая свои рисунки в тетрадях. Как часто бывает в процессе решения математических задач, они перемещались зигзагами, то приближаясь к нужному решению, то отдаляясь от него, а затем снова возвращаясь к нему (Лакатос, 2010). Разные подходы позволяли им тщательно исследовать математический ландшафт.

Я показывала видеозапись работы этих мальчиков на многих конференциях для учителей. На всех произвели впечатление их мотивация, настойчивость и высокий уровень дискуссии. Учителя знают, что настойчивость, которую продемонстрировали эти мальчики, а также уважительность, с которой они обсуждали идеи друг друга, особенно в летней школе, — явление весьма необычное, и им интересно, как мы этого добились. Им знакома ситуация, когда ученики (особенно отстающие) прекращают попытки, если задача трудная и им не удается получить ответ сразу. Но в нашем случае этого не произошло; когда мальчики не смогли двигаться дальше, они вернулись к своим диаграммам и обсудили друг с другом идеи, многие из которых были ошибочными, но в итоге все же смогли найти путь к решению. Показав видеозапись этого случая учителям во время конференции, я спрашиваю их, какие элементы взаимодействия учеников могут помочь нам понять причины высокого уровня их настойчивости и вовлеченности. Ниже представлен ряд важных соображений по поводу благоприятных возможностей для повышения вовлеченности всех учеников.

1. Задача трудная, но доступная.Все три мальчика смогли понять задачу, хотя им было нелегко. Она идеально соответствовала их уровню мышления. Найти задачи, которые идеально подойдут всем ученикам, трудно, но возможно, когда мы расширяем их: приводим к виду, который я называю «низкий пол, высокий потолок». Пол низкий, потому что все могут видеть, как растет фигура, а потолок высокий, поскольку функция, которую изучали мальчики, — квадратичная, с помощью которой шаг n может быть представлен в виде ( n + 1) 2блоков. Мы сделали «пол» ниже, предложив ученикам поразмышлять на визуальном уровне, хотя, как я покажу ниже, это не единственная причина для такой важной адаптации.

2. Мальчики восприняли задачу как головоломку, поэтому им было интересно искать решение. Вопрос не касался «реального мира» или жизни мальчиков, но увлек их. В этом и состоит сила абстрактной математики: она подразумевает открытое мышление и установление связей.

3. Рассуждения на визуальном уровне помогли мальчикам понять, как растет закономерность в задаче.Мальчики увидели, что представленная фигура растет как квадрат со стороной ( n + 1), рассмотрев рост закономерности визуально. Они искали сложное решение, но были уверены в себе: им помогало визуальное представление происходящего.

4. Мальчиков воодушевило, что каждый из них разработал свой способ визуального представления роста закономерностии все они нашли правильные методы, раскрывающие разные аспекты решения. Мальчики с воодушевлением поделились своими мыслями друг с другом и использовали свои идеи и идеи других при решении задачи.

5. Урок был организован так, чтобы ученики стремились предлагать идеи без страха совершить ошибку.Это позволило мальчикам двигаться дальше, когда они «застревали», предлагая идеи (и правильные, и ошибочные), которые позволят продолжить обсуждение.

6. Мы научили учеников уважать мнение друг друга. Мы призывали отдавать должное широте мышления каждого ученика, а не процедурному мышлению отдельных детей, а также давали высокую оценку разным способам визуального представления задач и установления связей.

7. Ученики использовали свои идеи, а не придерживались метода, взятого из учебника по алгебре. Они предложили разные идеи по поводу визуального представления роста функции, поэтому им было еще интереснее решать задачу.

8. Мальчики работали вместе.На видео заметно, как мальчики поняли друг друга, делясь идеями в процессе обсуждения, и получили еще большее удовольствие от работы.

9. Работа мальчиков носила смешанный характер.Люди, которые смотрят это видео, отмечают, что каждый ученик предлагает что-то особенное и по-своему важное. Сильный постоянно выкрикивает догадки по поводу чисел (эта стратегия могла бы быть полезной для сугубо процедурных вопросов), а слабые подталкивают его к тому, чтобы он размышлял на визуальном и более концептуальном уровне. Именно такое сочетание разных способов мышления помогает мальчикам и приводит их к успеху.

Как правило, в задачах на рост закономерности ученикам задают числовые вопросы вроде «Сколько кубиков на шаге 100?» и «Сколько кубиков на шаге n ?» Мы тоже поставили ученикам такие вопросы, но только после того, как они поработали над задачей сами, чтобы они проанализировали рост фигуры на визуальном уровне. Это изменило все.