Денис Соломатин - Математические модели в естественнонаучном образовании. Том II

Хотя алгоритм Фитча-Марголиаша позволил получить неравные длины ветвей в деревьях, за это заплатили высокую цену – построенные деревья оказываются некорневыми. Однако, поскольку поиск корня часто желателен, возникает необходимость обойти этот недостаток.

При применении любого метода филогенетического дерева, который дает некорневое дерево, может быть включен дополнительный таксон. Этот дополнительный таксон выбран так, чтобы было известно, что он более отдаленно связан с каждым из представляющих интерес таксонов, чем они связаны друг с другом, и присоединяется как внешняя группа. Например, если пытаемся связать разные виды уток друг с другом, то можем включить другой тип птиц в качестве внешней группы. Как только дерево без корней построено, находим корень такой, чтобы ребро из внешней группы соединялось с остальной частью дерева. Информация о том, что внешняя группа должна была отделена от других таксонов до того, как они отделились друг от друга, помогает определить место корня на дереве общего предка.

Задачи для самостоятельного решения:

5.2.1. Для дерева на рисунке 5.8, построенного методом UPGMA, вычислите таблицу расстояний между таксонами вдоль дерева. Как это соотносится с исходной таблицей данных расстояний?

5.2.2. Предположим, что четыре последовательност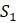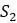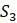и , , и 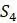ДНК разделены филогенетическими расстояниями, как показано в таблице 5.9. Создайте корневое дерево, показывающее отношения между 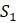, , 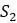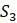и 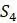с помощью UPGMA.

Таблица 5.9. Данные о расстоянии для задач 5.2.2 и 5.2.5

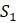
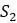
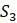
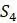
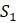
1.2 .9 1.7

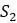
1.1 1.9

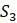
1.6

5.2.3. Выполните UPGMA для данных расстояния в таблице 5.4, которые были использованы в примере FM-алгоритма. Производит ли UPGMA топологически то же дерево, что и алгоритм FM? А метрически?

5.2.4. FM-алгоритм использует тот факт, что данные о расстоянии, относящиеся к трем терминальным таксонам, могут быть точно подогнаны по одному некорневому дереву, относящемуся к ним.

а. Выведите 3-точечных формулы, приведенные в разделе.

б. Если расстояния равны , и , то каковы длины , и ?

5.2.5. Используйте FM- алгоритм для построения некорневого дерева на данных в таблице 5.9, которая также использовалась в задаче 5.2.2. Насколько отличается получившийся результат?

5.2.6. Предположим, что три терминальных таксона связаны некорневым метрическим деревом.

а. Если три длины ребер равны 0.1, 0.2 и 0.3, объясните, почему гипотеза молекулярных часов должна быть неверной, независимо от того, где находится корень.

б. Если длины трех ребер равны 0.1, 0.1 и 0.2, объясните, почему гипотеза о молекулярных часах может быть верной. В случае, когда гипотеза оказывается верна, где должен находиться корень?

в. Если три длины ребер равны 0.1, 0.2 и 0.2, объясните, почему гипотеза молекулярных часов должна быть неверной, независимо от того, где находится корень.

5.2.7. В то время как данные о расстоянии для 3 терминальных таксонов могут точно соответствовать дереву без корней, при наличии 4 (или более) таксонов это обычно невозможно.

а. Нарисуйте некорневое дерево с терминальными таксонами A, B, C и D. Обозначьте длины пяти ребер .

б. Используя для расстояния между терминальными таксонами обозначения типа 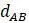, запишите уравнения для каждого из 6 таких расстояний выраженных через . Объясните, почему, если даны числовые значения расстояний между терминальными таксонами, эти уравнения вряд ли будут иметь точное решение.

в. Приведите такой конкретный пример значений 6 расстояний между терминальными таксонами, чтобы уравнения в части (б) не могли иметь точного решения. Приведите еще один пример значений, для которых уравнения могут быть решены.

5.2.8. Известен ряд различных мер для оценки степени согласованности между данными о расстояниях и метрическими деревьями. Пусть обозначает расстояние между таксонам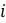и и , полученное из экспериментальных данных, а обозначает расстояние, полученное при обходе от 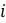до вдоль дерева. Во второй половине прошлого века были предложены следующие три меры:

(Фитч и Марголиаш, 1967)

(Фаррис, 1972)

(Татено и др. , 1982)

Во всех этих мерах суммы включают слагаемые для каждой отдельной пары таксонов 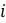и .

а. Вычислите эти меры для дерева, построенного в разделе, используя FM- алгоритм, а также дерева, построенного из тех же данных с помощью UPGMA в задаче 5.2.3. Согласно каждому из этих показателей, какое из двух деревьев лучше подходит для данных?

б. Объясните, почему эти формулы разумно использовать для оценки соответствия. Объясните, как различия между формулами делают их более или менее чувствительными к различным типам ошибок.