Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]

Предложите ребенку улучшить показатели по таблице умножения. Сначала выберите, с каким разделом вы будете работать, допустим, это будет умножение на 3. В таблице, которую он должен заполнить за 3 минуты, в 48 графах стоят числа, которые ему предстоит умножить на 3 и записать результат. Дальше переворачивайте песочные часы или ставьте таймер и командуйте: «На старт, внимание… марш!»

Сколько правильных ответов у него получилось за 3 минуты? Это лучше или хуже, чем в прошлый раз? Стремление улучшить предыдущий результат придаст этому занятию дополнительный азарт. Можно использовать секундомер, чтобы было понятнее, с какой скоростью ребенок считает. Не забывайте о статистике, результаты надо фиксировать. И учтите, что лучшее время – вопрос недель, а то и месяцев упражнений.

На разговоры о математике нас может натолкнуть что угодно, будь то колпак на колесо автомобиля или качели на детской площадке. Постарайтесь помочь ребенку увидеть математику вокруг: в парке, в саду, на улице.

Способствует навыку распознавания фигур и вероятностного прогнозирования.

Когда вы в последний раз разглядывали колпаки на колесах автомобилей или крышки канализационных люков? Если вы нормальный человек, а не псих-одиночка, то скорее всего вы вообще ни разу их не разглядывали. Но именно этим мы и хотим предложить вам заняться, потому что колпаки и крышки люков дают интереснейшую пищу для математических размышлений о повторяемости форм.

Вы идете по улице, и мимо вас проезжает автомобиль. Какие у него колпаки на колесах? Сколько там спиц? Пять? А может, не пять, а шесть? И они расходятся, как лучи изящной звезды? А может, никаких спиц нет? Может, там прорези? И сколько их, восемь? А как назвать фигуру, которую они образуют?

На крышке канализационного люка выпуклости и борозды складываются в определенный узор, который тут неспроста. Он на всех люках один и тот же или меняется? Может, это шифр или тайнопись?

К слову сказать, хорошо, что эти крышки круглые, а не квадратные, ведь стороны круглой крышки и люка всегда совпадут, как ни поверни, а значит, больше вероятность, что крышка надежно лежит на месте. Кроме того, квадратная крышка могла бы провалиться внутрь люка, если повернуть ее на ребро, взять за верхний угол и опускать по диагонали. А раз она круглая, есть гарантия, что она ни при каких обстоятельствах не провалится внутрь, ведь продольный и поперечный диаметры окружности равны.

Способствует изучению свойств треугольников, развитию измерительных и оценочных навыков.

Если есть маршрут, по которому вы с ребенком регулярно ходите – например от дома до школы или до магазина, – попробуйте вместе поискать кратчайший путь. Дорога, предполагающая переход на противоположную сторону улицы, – это просто подарок судьбы, тогда преимущества будут особенно наглядными.

Что быстрее: двигаться без затей вдоль гигантской буквы Г или сновать как челнок, мелкими перебежками вправо-влево, срезая углы? Ответ на этот вопрос могут дать только тщательные измерения. Для этого придется посчитать шаги, но надо стараться, чтобы длина шага была одной и той же. Подсчет доверьте шагомеру или установите на свой смартфон специальное приложение (хотя точность может вызывать сомнения).

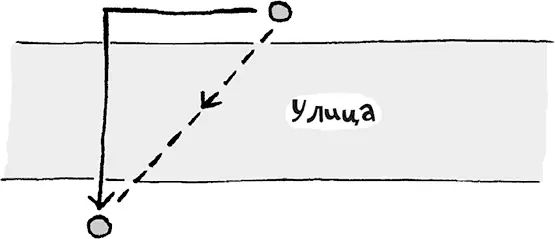
Если улица, которую надо переходить, спокойная, попробуйте пересечь ее по диагонали, как показано на рисунке. Посмотрите, насколько пунктирная линия короче сплошной!

Раз выгода движения по диагонали стала очевидной, постарайтесь найти кратчайшую диагональ. (Подсказка: лучший способ срезать путь через поле, двор или площадь – это движение по биссектрисе, путь получится короче на треть.)

Это занятие непременно понравится вашему ребенку и исподволь введет его в мир прямоугольных треугольников и теоремы Пифагора, который ему предстоит изучить вдоль и поперек, когда он станет постарше.

Способствует восприятию времени, усвоению причинно-следственных связей, развивает вероятностное прогнозирование.

Если на прогулку в парке вы взяли с собой мяч, можно понаблюдать за тем, как он скачет. Бросьте мяч и посчитайте, сколько раз он подпрыгнет, прежде чем остановится.

Вот несколько вопросов, над которыми интересно поразмышлять вместе с ребенком:

• Как заставить мяч прыгать дольше?

• Что будет, если подбросить его повыше?

• Что будет, если ударить его о землю с большей силой?

• Если у вас с собой два мяча, какой из них перестанет скакать и остановится первым?

• Когда мяч скачет, как он это делает? Должен ли обязательно существовать зазор между мячом и землей?

Любопытнее всего последить за временными промежутками между отскоками. Они становятся все короче и короче. Может, потому что мяч начинает прыгать все быстрее и быстрее и под конец настолько быстро, запредельно быстро, что… останавливается?

Способствует формированию понятия «кривая».

Во время любых игр с мячом привлеките внимание ребенка к траектории полета. Можно ли сказать, что мяч летит по прямой? Наверняка ребенок и сам заметит, что путь мяча в воздухе представляет собой кривую – но что это за кривая? Как ее описать?

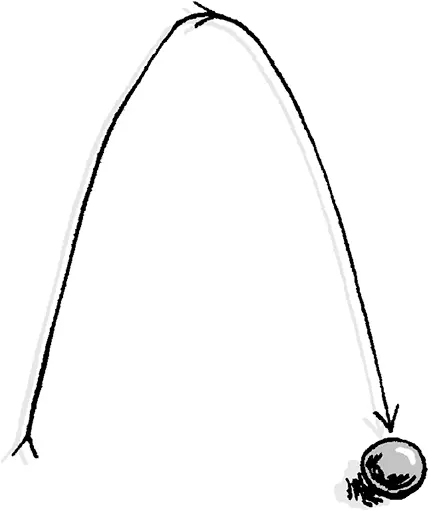
Самая знакомая для ребенка форма кривой – это окружность.

– Может, мяч делает в воздухе круг? Но если он летит по кругу, то должен лететь-лететь-лететь, потом сделать такую петлю и вернуться к тому, кто его бросил, а этого почему-то не происходит. («Это он на землю натыкается», – сказал один маленький мальчик.)