Роб Истуэй - Математика на ходу [Более 100 математических игр для больших и маленьких] [litres]

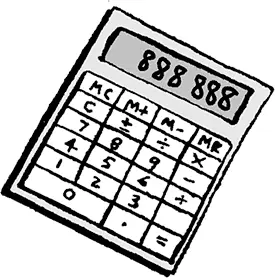
Ребенок.37!

Родитель.Абракадабра 37!!! Дальше?

Добавив в калькулятор последнее число, а это 11, сделайте пассы руками, произнесите что-то вроде «Крибле-крабле-бумс!» и нажмите на кнопку «равно». Возраст ребенка появится на дисплее 6 раз: 888 888!

(Если ребенку 10 лет или больше, он все равно оценит этот фокус, но уже не с возрастом. Просто попросите его выбрать любое число от 1 до 9.)

Вам понадобятся бумага, ножницы, клейкая лента.

Способствует развитию представлений о форме и гранях поверхностей.

Отрежьте или аккуратно оторвите от длинной стороны листа бумаги полоску шириной в 4 см. Начертите посередине сверху донизу пунктирную линию, пусть будет похожа на дорожную разметку. Теперь соедините верхний и нижний концы полоски с помощью клейкой ленты, но не забудьте предварительно перевернуть один из них, как показано на рисунке. Все, факир готов работать, приступаем.

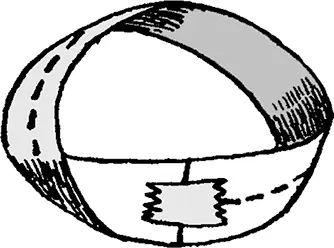
Вы говорите ребенку, что собираетесь разрезать ножницами кольцо вдоль пунктирной линии, и спрашиваете:

– Если я разрежу одно кольцо на две части, сколько у меня в результате получится колец?

– Два, – отвечает не чувствующий подвоха ребенок, и по логике вещей он прав.

– Это когда оно простое. А это кольцо волшебное.

Вы начинаете аккуратно резать по разметке и, когда делаете последнее движение ножницами, из одного широкого кольца у вас получается… одно, только в два раза длиннее и у́же.

А все потому, что у вас в руках была поразительная лента Мёбиуса, обладающая массой удивительнейших свойств. Представьте себе, что по ней ползет муравей-неряха, который не очень хорошо вытер ноги, поэтому он оставляют следы. Вот наш муравей (это ваши пальцы) ползет посередине ленты (вдоль пунктирной разметки), и всюду остаются его грязные следы (это точки, которые вы ставите ручкой или карандашом), вот он идет, идет, пока не доходит до того места, откуда начал свой путь. Но почему его следы оказались на обеих сторонах ленты? Он ведь двигался только по одной стороне, через край не перелезал, в чем же дело?

А дело в том, что у ленты Мёбиуса не две поверхности, а одна, то есть она односторонняя. В этом без труда можно убедиться, проведя пальцем по всей ее длине.

Если зритель требует еще чудес, посмотрите, что будет, если перед склеиванием перекрутить один из концов ленты не один раз, а два, а потом, как в предыдущем случае, разрезать ленту вдоль разметки посередине.

Но еще интереснее будет, если взять обычную ленту Мёбиуса и начать разрезать ее вдоль, отступив на ⅓ от края.

Вам понадобятся числовые кубики (не менее 3 штук).

Способствует развитию счетных навыков, особенно умножению на 7.

Ребенок суммирует значения «невидимых» верхних и нижних поверхностей

Эту игру легко освоит любой ребенок, а заодно он выучит таблицу умножения на 7 и поупражняется в вычитании.

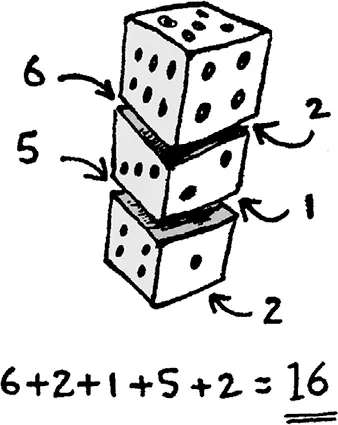
Для начала попросите поставить один на другой три числовых кубика. Пока башня строится, вы стоите спиной, потом поворачиваетесь и предлагаете:

– Спорим, я умею видеть сквозь предметы? Вот у нас три кубика, они стоят один на другом, поэтому есть поверхности, которых я не вижу. Их пять. Но я могу силой взгляда увидеть числа на закрытых поверхностях, сложить вместе и назвать сумму.

Слово с делом у вас не расходится, поэтому вы записываете результат и, не показывая ребенку, откладываете его в сторону. Потом вместе с ним смотрите, что было на закрытых поверхностях, и складываете открывшиеся числа. Допустим, это 6 + 2 + 5 + 1 + 2 = 16. После этого вы медленно и торжественно разворачиваете листок с записанным заранее результатом, а там… 16!

Разоблачение: две параллельные поверхности кубика в сумме всегда дают 7. Таким образом, 3 пары верхних и нижних поверхностей в совокупности дадут 21, потому что 3 × 7 = 21. Все, что требуется, – это вычесть из суммы значение «макушки», единственной поверхности, которая нам видна. На рисунке это 5, следовательно, 21 – 5 = 16.

Этот эффектный фокус можно проделывать с любым количеством кубиков. Если их будет 6, то 6 × 7 = 42, а потом вычитаете из произведения значение «макушки» и… готово!

Способствует распознаванию форм и усвоению понятия симметрии.

Переверните эту страницу вверх ногами и прочитайте ее в зеркале. Слово QUALITY превратится в полную абракадабру, а вот слову CHOICE все нипочем. Почему так?

Если ваш ребенок знает английский, предложите ему поискать другие слова, которые можно читать в зеркале. Какое из них будет самым длинным? (Наш результат – KICKBOXED, хотя в словарях вы его вряд ли найдете [17].)

Вам понадобятся бумага и карандаш.

Способствует развитию счетных навыков и механизма вероятностного прогнозирования.

Попросите ребенка задумать и записать двузначное число. Предположим, это будет 49. Теперь он должен сложить между собой обе цифры, то есть 4 и 9, и сказать вам сумму. В нашем случае это 13. От вас требуется лишь умножить в уме названное вам число на 11 ( см. п. 41) и записать результат. В нашем случае это будет 143.

Далее вы просите ребенка превратить задуманное число (не называя его вам!) в перевертыш, то есть из 49 сделать 94, и сложить исходное число и перевертыш. И раз вы уже записали свое предсказание, можете помочь ребенку в подсчетах: 49 + 94 = 143.

Под гром оваций обнародуйте свое предсказание.