Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

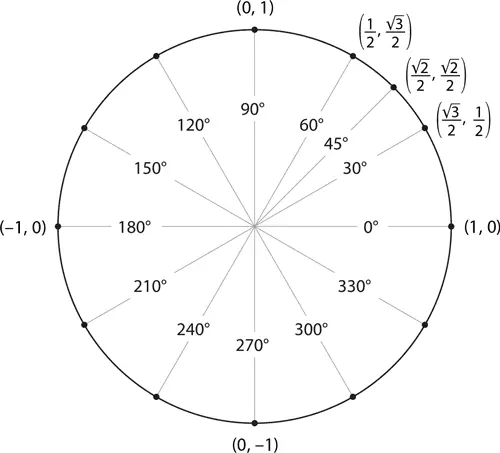
Прибавление или вычитание 360° на величину угла никак не повлияет (мы просто обойдем вокруг него с одной или другой стороны), а значит, для любого ∠ A

Имея дело с отрицательными значениями углов, мы двигаемся по окружности слева направо: так, угол, равный –30°, ничем, по сути, не отличается от угла, равного 330°. Обратите внимание, что сдвиг на A градусов по часовой стрелке приводит нас к той же x -координате, что и сдвиг на те же A градусов против часовой стрелки. Y -координата же при этом сменит знак на противоположный. Другими словами, для любого значения угла A

Например,

Обратное происходит, когда мы «отзеркаливаем» ∠ A через ось y . Значение y -координаты получившегося таким образом дополнительного угла 180 – A остается неизменным, а значение x -координаты меняет знак на противоположный. То есть

Скажем, при A = 30°

Остальные тригонометрические функции определяются по старой схеме (например, tan A = sin A /cos A ).

Оси x и y «разрезают» поверхность окружности на четыре сектора-квадранта . Пронумеруем их римскими цифрами по часовой стрелке – I, II, III и IV, – начиная с правой верхней, то есть с диапазона углов от 0° до 90°. Квадрант II, таким образом, охватит диапазон от 90° до 180°, квадрант III – от 180° до 270°, а квадрант IV – от 270° до 360°. Обратите внимание, что в разных квадрантах разные тригонометрические функции будут вести себя по-разному: положительные значения синуса мы получим в квадрантах I и II, косинуса – в квадрантах I и IV, тангенса – в квадрантах I и III. Чтобы это запомнить, некоторые из моих учеников любят повторять «Все студенты таскают калькуляторы» (посмотрите на первые буквы в каждом слове этой «запоминалки»: «в» – «все функции» в квадранте I, «с» – «синусы» в квадранте II, «т» – «тангенсы» в квадранте III, «к» – «косинусы» в квадранте IV).

Ну и еще немного терминологии. Для определения неизвестных значений углов нужны обратные тригонометрические ( циклометрические, круговые ) функции . Например, обратным синусом 1/2 будет sin –1(1/2) [32]. Такого рода функция говорит нам, что мы имеем дело с неким ∠ A , синус которого равен 1/2. А так как мы знаем, что sin 30° = 1/2, получаем

Функция sin –1(которая также называется арксинусом ) всегда даст нам угол в диапазоне от –90° до 90°, но мы-то с вами знаем, что есть и другие углы с тем же значением синуса – синус 150°, например, будет также равен 1/2. То же происходит и с любым кратным 360° значением, прибавляемым к 30° или 150° – синусы будут равны.

Для треугольника с длинами сторон 3, 4 и 5 (см. рисунок) калькулятор может рассчитать ∠ A тремя различными способами, каждый из которых будет основан на своей обратной функции:

Самое время применять все эти знания на деле. В «геометрической» главе мы доказали теорему Пифагора, с помощью которой можно вычислить длину гипотенузы прямоугольного треугольника, зная длины его катетов. Здесь же, в главе «тригонометрической», мы можем сделать практически то же самое для любого треугольника. В этом нам поможет закон косинусов.

Теорема (закон косинусов):Длина стороны c любого треугольника ABC , в котором стороны a и b образуют ∠ C , соответствует

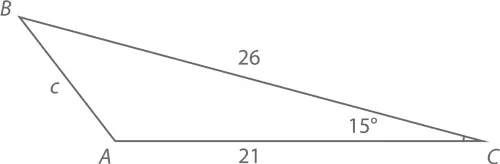
Для примера взгляните на изображенный ниже треугольник ABC . Между двумя его сторонами с длинами 21 и 26 лежит угол 15°. Согласно закону косинусов, длина третьей стороны с составит

А так как cos 15° ≈ 0,9659, уравнение упрощается сначала до c ² = 62,21, а потом и до c ≈ 7,89.

Доказательство:Чтобы доказать эту теорему, рассмотрим три частных случая – в зависимости от того, будет ли ∠ C прямым, острым или тупым. Если ∠ C – прямой, его косинус будет равен cos 90° = 0, что упрощает закон косинусов до c ² = a ² + b ², то есть до уже доказанной нами теоремы Пифагора.

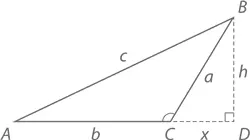
Если ∠ C – острый (как на рисунке), опустим перпендикуляр из ∠ B к стороне AC до лежащей на ней точки D . Получим два треугольника. Применим теорему Пифагора к CBD – a ² = h ² + x ² и придем к

Треугольник же ABD можно просчитать как c ² = h ² + ( b – x )² = h ² + b ² – 2 bx + x ², то есть

Составим из двух равных h ² частей уравнение:

Следовательно,

В треугольнике CBD cos C = x / a , поэтому x = a cos C . Следовательно, если ∠ C является острым, то

Если же ∠ C – тупой, дополним треугольник ABC прямоугольным треугольником CBD , как на рисунке:

Для него, как и для получившегося большого, верна теорема Пифагора: a ² = h ² + x ² и c ² = h ² + ( b + x )². Как и в случае с острым ∠ C , соединим уравнения: