Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

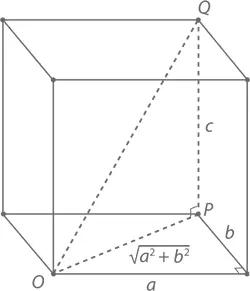
Теперь проложим линию c от точки P к точке Q , образующей угол, противолежащий O . Чтобы найти расстояние от O до Q , нам понадобятся длины катетов прямоугольного треугольника 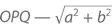и c . Применим к ним теорему Пифагора и получим, что длина диагонали OQ равна

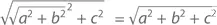
Ну а теперь собственно тождество – столь же полезное, сколь и красивое. Доказательство может показаться несколько запутанным, поэтому можете смело его пропускать (хотя я все же советую вам в нем разобраться – оно ляжет в основу доказательства других тождеств).

Теорема:Для любых углов A и B

Доказательство:На единичной окружности, центром которой является точка O , расположены точки P (cos A , sin A ) и Q (cos B , sin B ). Предположим, что длина отрезка PQ равна с . Что можно сказать о ней?

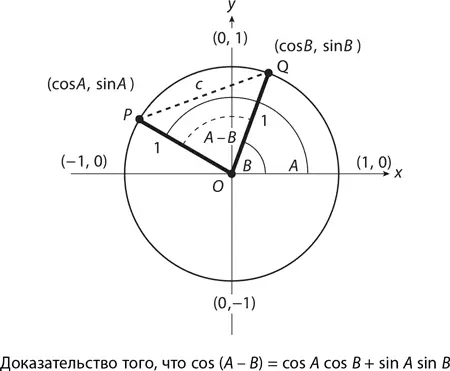
В треугольнике OPQ отрезки OP и OQ являются радиусами единичной окружности, а значит, их длина равна 1, а ∠ POQ может быть измерен как A – B . Следовательно, согласно закону косинусов,

С другой стороны, формула расстояния приводит нас к уравнению

поэтому расстояние c от точки P = (cos A , sin A ) до точки Q = (cos B , sin B ) соответствует

где последнее представление основывается на уравнениях cos² B + sin² B = 1 и cos² A + sin² A = 1.

Соединив эти уравнения для c ², получаем

Вычтем из обеих частей 2, разделим их на –2 и получим

что и требовалось доказать.◻

Формула для cos ( A – B ) основывается на законе косинусов и исходит из того, что 0° < A – B < 180°. Но ту же теорему можно доказать и выйдя за рамки подобных ограничений. Если переместить треугольник POQ по часовой стрелке на B градусов, мы получим конгруэнтный ему треугольник P'OQ' , в котором Q' будет располагаться на оси x в координатах (1, 0).

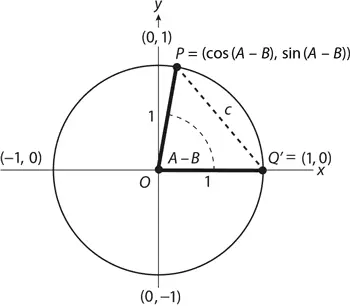
Так как ∠ P'OQ' = A – B, P' = (cos ( A – B ), sin ( A – B )). Согласно формуле расстояния для P'Q' будет верно следующее:

c ² = (cos ( A – B ) – 1)² + (sin ( A – B ) – 0)² = cos² ( A – B ) – 2 cos ( A – B ) + 1 + sin² ( A – B ) = 2 – 2 cos ( A – B )

Из этого можно заключить, что c ² = 2 – 2 cos ( A – B ), при этом нам не нужны ни теорема косинусов, ни предположение об угле A – B . Ну а дальнейшее доказательство можно скопировать с предыдущего.

Обратите внимание, что при A = 90° формула для cos ( A – B ) утверждает следующее:

Происходит это на том основании, что cos 90° = 0, а sin 90° = 1. Если в этом уравнении заменить B на 90° – B , получим

Мы уже доказали правдивость этих утверждений на примере B как острого угла. Однако алгебра позволяет нам пойти дальше и подтвердить их для любого значения B . Так, если заменить B на – B , мы придем к

так как cos (– B ) = cos B , а sin (– B ) = –sin B . Если предположить, что B = A , у нас получится формула функций двойного угла :

А так как cos² A = 1 – sin² A и sin² A = 1 – cos² A , мы также можем утверждать, что

Из этого тождества косинусов проистекает аналогичное тождество синусов, например,

B = A приводит нас к формуле функций двойного угла для синусов –

а замена B на – B – к

Давайте соберем в одну таблицу все тождества, которые мы успели вывести в этой главе: