Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

В треугольнике CBD cos (180° – C ) = x / a , то есть x = a cos (180° – C ) = – a cos C . И мы вновь приходим к искомому:

Кроме того с помощью функций можно рассчитать площадь треугольника.

Сопутствующая теорема:В любом треугольнике ABC со сторонами a и b и лежащим между ними ∠ C

Доказательство:Площадь треугольника с длиной основания b и высотой h равна 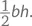Все три треугольника, рассмотренные при доказательстве закона косинусов, имеют основание b . Определим высоту h . В остроугольном треугольнике обратим внимание на то, что sin C = h / a , то есть h = a sin C . В тупоугольном треугольнике sin (180° – C ) = h / a , поэтому опять имеем h = a sin (180° – C ) = a sin C . В прямоугольном же треугольнике h = a , что равно a sin C , потому что C = 90°, а sin 90° = 1. Следовательно, так как во всех трех случаях h = a sin C , площадь треугольников составит 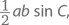что и требовалось доказать.

Следствия этой теоремы очевидны:

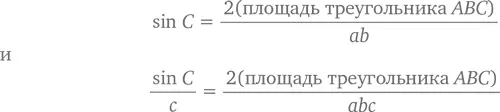
Другими словами, в треугольнике ABC (sin C )/ c равен его удвоенной площади, разделенной на произведение длин трех его сторон. Какой угол выбрать, по большому счету не так уж и важно – (sin B )/ b или (sin A )/ a дадут нам тот же результат. И это доказывает одну очень полезную теорему.

Теорема (закон синусов):В любом треугольнике ABC , длины сторон которого соответственно равны a, b и c ,

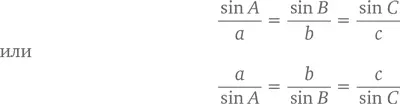
Закон синусов – это еще один способ вычислить высоту нашей горы. На этот раз мы сосредоточимся на a – диагонали, пролегающей между нами и вершиной:

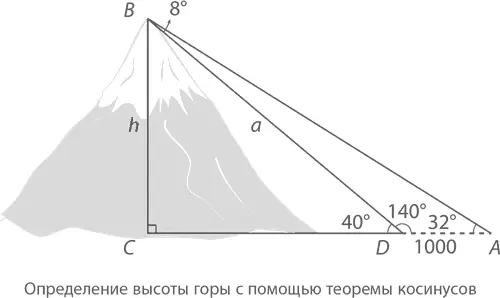
Способ № 5 (закон синусов): В треугольнике ABD ∠ BAD = 32°, а ∠ BDA = 180° – 40° = 140°. Следовательно, ∠ ABD = 8°. Согласно закону синусов получаем

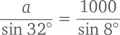
Умножим обе части на sin 32°, что даст нам a = 300 sin 32°/ sin 8° ≈ 1143 метров. А так как sin 40 ≈ 0,6428 = h / a , то

что полностью совпадает с ответом, к которому мы пришли в прошлом разделе.

Не менее замечательна в этом отношении формула Герона , с помощью которой можно найти площадь треугольника по длинам его сторон a, b и c . Сначала мы находим полупериметр p :

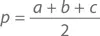
А потом и площадь S :

Например, если взять треугольник со сторонами 3, 14 и 15 (узнаете первые пять цифр числа π?), полупериметр будет равен (3 + 14 + 15)/2 = 16, а площадь, таким образом, – √( 16(16 – 3)(16 – 14)(16 – 15) ) = √ 416 ≈ 20,4 .

Несложно, правда? Уверен, внимательный читатель не сможет не заметить здесь закон косинусов, слегка приправленный алгеброй.

Но этим возможности тригонометрических функций не ограничиваются. Они способны и на куда более интересные и запутанные взаимоотношения – так называемые тождества . Некоторые из таких тождеств мы уже наблюдали, например,

Но их, конечно же, куда больше.

Из тождеств рождаются формулы, притом весьма полезные. Ими-то мы и займемся в этом разделе.

Первое тождество основывается на формуле единичной окружности:

Под эту формулу должна подходить точка (cos A , sin A ), принадлежащая единичной окружности. Следовательно, (cos A )² + (sin A )² = 1, из чего проистекает, пожалуй, наиболее важное тригонометрическое тождество.

Теорема:Для любого ∠ A

До сих пор все произвольные углы мы обозначали буквой A . Но это не значит, что вы обязаны всегда так делать, можно брать и другие буквы, например, x :

В тригонометрии для этой цели часто используется греческая буква θ (тета) –

А бывает и так, что вообще ничего не используется:

Но перед тем как доказывать какое бы то ни было тождество, нужно найти длину отрезка прямой. В этом нам поможет теорема Пифагора.

Теорема (формула расстояния между двумя точками):Обозначим длину отрезка прямой от точки ( x 1, y 1) до точки ( x 2, y 2) буквой L . Тогда

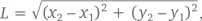
Например, длина отрезка от точки (–2, 3) до точки (5, 8) равна

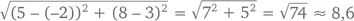
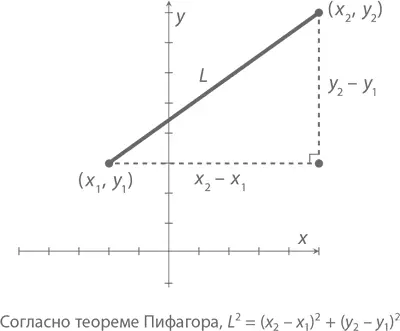
Доказательство:Возьмем две точки ( x 1, y 1) и ( x 2, y 2). Начертим прямоугольный треугольник, гипотенузой которого будет отрезок, соединяющий эти точки. На рисунке выше длина основания равна x 2 – x 1, а высота – y 2 – y 1. Следовательно, согласно теореме Пифагора, гипотенуза L равна

то есть 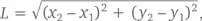что и требовалось доказать.

Чему будет равна диагональ в коробке размером a × b × c ? Возьмем прямоугольник, образующий дно этой коробки, и обозначим пару противоположных его углов буквами O и P . Длина и ширина при этом будут равны соответственно a и b , а диагональ OP – √( a ² + b ²).