Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Некоторые даже называют ее «уравнением Бога», ведь в ней сошлись вместе пять фундаментальных констант, пять самых важных чисел математики: 0 и 1 – начала всех арифметических начал, π, позволяющее постичь геометрию, e , открывающее врата во вселенную исчисления, и i , из которого произрастает древо алгебры.

В нем прекрасны и отношения между этими числами: сложение, умножение и возведение в степень – все то, что символизирует рост.

О ноле, единице и π мы уже кое-что знаем, самое время разобраться с иррациональным e и мнимым i . А когда разберемся, вы удивитесь, насколько простым вам покажется тождество Эйлера, буквально как 1 + 1 = 2 (ну или хотя бы как cos 180° = –1).

А вот еще несколько постоянных претендентов на корону самой красивой формулы. Большинство из них уже встречались вам на уже прочитанных страницах или скоро встретятся на непрочитанных. Первые два также рождены гением Леонарда Эйлера.

Загадочная природа числа i кроется в формуле

На первый взгляд это кажется совершенно невозможным: разве может быть отрицательным число, умноженное несколько раз на само себя? В конце концов, даже 0² = 0, а любая возведенная в квадрат отрицательная величина обязана стать положительной, разве нет? Не спешите рубить с плеча. Вспомните, ведь было такое время, когда вы вообще ничего не знали об отрицательных числах, да и, узнав, вряд ли сразу же поверили в их существование (как и многие-многие математики до вас). Что это вообще за глупость – количество, меньшее, чем 0? Как что-то может быть меньше, чем ничто ? Но потом в вашей жизни появляется некая ось (вроде той, что изображена чуть ниже), а вместе с ней – и все ее обитатели: положительные значения, расположившиеся справа от 0, и отрицательные значения, расположившиеся слева. В точно таком же, нестандартном ключе нам следует рассматривать и число i – тогда-то нам и откроется его истинное, реальное значение.

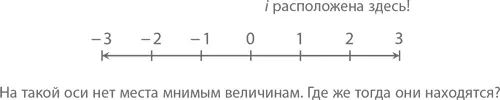
Число i считается мнимым – таким, которое при возведении в квадрат дает отрицательный результат. Мнимое число 2 i , например, дает (2 i )(2 i ) = 4 i ² = –4.

В алгебраическом смысле мнимые числа ничем не отличаются от чисел действительных. Судите сами:

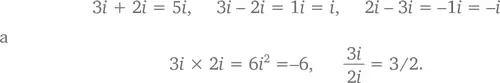
Кстати, если взять и возвести в квадрат – i , получится тот же результат (–1), потому что (– i )(– i ) = i ² = –1. Не менее предсказуемы и последствия перемножения мнимого и действительного чисел – скажем, 3 × 2 i = 6 i .

А что со сложением? Чему, например, равна сумма 3 и 4 i ? Очевидно, что 3 + 4 i , и дальше с этим ничего сделать нельзя (равно как и ничего нельзя сделать с 1 +√ 3 ). Числа, образованные по модели a + bi (где a и b суть действительные величины), называются комплексными . Получается, что любая величина, будь она действительной (при b = 0) или мнимой (при a = 0), есть, по своей сути, особая форма комплексного числа. То есть действительное π и мнимое 7 i будут также комплексными.

Давайте попробуем разобраться в этом с помощью нескольких конкретных примеров. Начнем со сложения и вычитания:

Для умножения применим алгебраический метод FOIL , описанный в главе 2:

Для комплексного числа каждый квадратный многочлен ax ² + bx + c будет иметь два корня (или же один, но повторяющийся). Согласно формуле корней квадратного уравнения, многочлен будет равен 0 всякий раз, когда

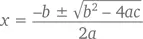
Помните, в главе 2 мы с вами говорили о том, что нельзя извлечь квадратный корень из отрицательной величины? Но ведь никакие квадратные корни отрицательных величин нам и не нужны. Смотрите сами: уравнение x ² + 2 x + 5, например, имеет корни

Кстати, формула корней квадратного уравнения будет верна даже при комплексных значениях a, b или c .

В любом квадратном многочлене мы можем найти как минимум один корень, пусть и комплексный. На этот счет есть своя теорема.

Теорема (основная теорема алгебры):Любой многочлен p ( x ), возводимый в первую или бо́льшую степень, имеет корень z при p ( z ) = 0.

Обратите внимание, что многочлен первой степени, вроде 3 x – 6, может быть представлен как 3( x – 2), где 2 есть единственный корень 3 x – 6. Обобщая, можно сказать, что при a ≠ 0 многочлен ax – b можно представить в виде a ( x – ( b / a )), где b / a будет являться корнем ax – b .

То же происходит и с многочленами второй степени: разложив ax ² + bx + c до a ( x – z 1)( x – z 2), мы получаем его корни – z 1и z 2(они вполне могут оказаться комплексными величинами, равно как и одной и той же величиной). И так можно продолжать до бесконечности – с любым многочленом любой степени.

Сопутствующая теорема:Любой многочлен степени n ≥ 1 может быть разложен на n составляющих. А именно: если p ( x ) есть многочлен n -ной степени, в котором главный член a ≠ 0, должно существовать n чисел z 1, z 2…., zn (которые вполне могут оказаться комплексными величинами, равно как и одной и той же величиной), соответствующих p ( x ) = a ( x – z 1)( x – z 2)… ( x – z n). Величины z i являются корнями многочлена при p ( z i) = 0.

Теорема эта означает, что любой многочлен степени n ≥ 1 будет иметь как минимум один и как максимум n различных корней.

Например, x 4 – 16 есть многочлен четвертой степени. Следовательно, его можно разложить как

из чего очень хорошо видно, что у него будет четыре различных корня: 2, –2, 2 i , – 2 i .