Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Одной из причин популярности логарифмов является их уникальная способность преобразовывать огромные значения в малые, куда более удобоваримые для человеческого ума. Логарифмы, в частности, используются при измерении и подсчете магнитуды землетрясения по шкале от 1 до 10 (да-да, это я о знаменитой шкале Рихтера), громкости звука (в децибелах), кислотности химических растворов ( pH ) и даже рейтинга посещаемости интернет-страниц (в алгоритме PageRank , придуманном корпорацией Google ).

Что собой представляет lg 512? Любой профессиональный калькулятор (равно как и большинство поисковых систем в Интернете) скажет вам, что log 512 = 2,709…. Вполне похоже на правду: 512 находится между 10² и 10³, а значит, его логарифм должен быть больше 2, но меньше 3.

Логарифмы были изобретены для того, чтобы преобразовывать умножение в более простое сложение. Основано это на одной любопытной теореме.

Теорема:Для любых положительных значений x и y

Другими словами, логарифм произведения равен сумме логарифмов .

Доказательство:Согласно правилам действий со степенями,

Следовательно, возведение 10 в степень lg x + lg y дает xy , что и требовалось доказать.◻

Не менее полезно следующее правило.

Теорема:Для любого положительного значения x и любого целого значения n

Доказательство:Согласно правилам действий со степенями, a bc = ( a b ) c . Следовательно,

то есть логарифм x n равен n lg x .◻

Десятичный логарифм – штука вполне себе обычная, насколько вообще обычным может быть нечто столь активно использующееся в таких важных областях науки, как химия, физика или геология (справедливости ради все же следует упомянуть, что в информатике и дискретной математике предпочтение отдается логарифму с основанием 2). В целом же для любого значения b > 0 логарифм по основанию b log b определяется согласно следующему правилу

Так, log 232 = 5, потому что 2 5= 32. А все уже рассмотренные нами свойства логарифмов соответствуют любому значению b . Так, например,

В большинстве разделов математики, физики и техники самым полезным считается логарифм по основанию b = e . Он называется натуральным и даже имеет свое специальное обозначение – ln x . То есть

Или же, для всех действительных значений x ,

Ваш калькулятор, например, может за долю секунды подсчитать, что ln 5 = 1,609…, однако это нам уже хорошо известно по тому, что e 1,609≈ 5. Подробнее же о функциях натурального логарифма мы поговорим в главе 11.

Большинство профессиональных калькуляторов способно считать как натуральные, так и десятичные логарифмы. И лишь очень немногие ориентированы на другие значения b . Впрочем, проблемы тут никакой нет: одно основание довольно легко преобразовать в другое. Да-да, один логарифм является ключом ко всем остальным! На этот счет даже есть своя теорема, благодаря которой мы можем, например, взять логарифм по основанию 10 и найти его аналог по основанию b .

Теорема:Для любых положительных значений b и x

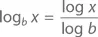
Доказательство:Предположим, что y = log b x . Тогда b y= x . Прологарифмируем обе части: log b y= log x . Согласно второму замечательному пределу, y log b = log x . Следовательно, y = (log x )/(log b ), что и требовалось доказать.◻

log b x = (log x ) / (log 2) = (log x ) / (0,301…) ≈ 3,32 log x

Как и число π, число e широко используется в математике. И, как и π, оно встречается подчас там, где вы совершенно не ожидаете его увидеть. Например, колоколообразная кривая, которую мы уже упоминали в главе 8, имеет формулу

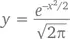
а ее график, изображенный чуть ниже, – наверное, самый важный график в любом статистическом исследовании.

В той же главе 8 мы встречали e в формуле Стирлинга для множества n !:

Позже, в главе 11, на примере e x и бесконечной последовательности

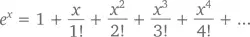
мы увидим важную связь между числом e и факториальным многочленом.

В частности, при x = 1,

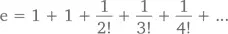
Не правда ли, очень легкий и быстрый способ определить цифры, составляющие число e ?

Кстати, о цифрах… Вы наверняка уже заметили, что число e начинается с повторяющейся последовательности цифр

или, как любил повторять один мой преподаватель, «2,7 Эндрю Джексон, Эндрю Джексон», потому что седьмой президент США был избран именно в 1828 году. («Запоминалка» эта, кстати, отлично подходит и студентам-историкам: с помощью первых цифр числа e можно запомнить год избрания Джексона.) [33]Как тут не усомниться в иррациональной природе e ? Ведь если бы последовательность 1828 повторялась бесконечно, e было бы обычным рациональным числом. Но нет, дальше идут 6 цифр… 459045… (лично я запомнил их как значения углов равнобедренного прямоугольного треугольника).