Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

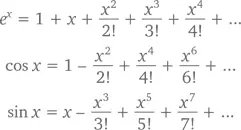
Считалось, что эти формулы работают при любых действительных значениях x . Эйлеру же хватило дерзости предположить, что они будут истинны и при мнимых значениях х . Задавшись вопросом, что произойдет, если возвести число в степень мнимого числа, он сформулировал свою известную теорему.

Теорема Эйлера:Для любого значения угла θ (выраженного в радианах)

Доказательство:Посмотрим, что будет происходить с последовательностью для e xпри x = i θ:

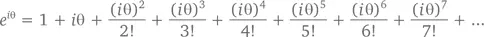
Обратите внимание на поведение i при возведении его в последовательные степени: i 0= 1, i 1= i, i 2= –1, i 3= – i (последнее потому, что i 3= i 2 i = – i ). Затем закономерность повторяется: i 4= 1, i 5= i, i 6= –1, i 7= – i, i 8= 1 и т. д. Еще более пристальное внимание следует обратить на то, что среди полученных результатов последовательно чередуются действительные и мнимые величины, что дает нам возможность выносить число i за скобки при каждом втором шаге:

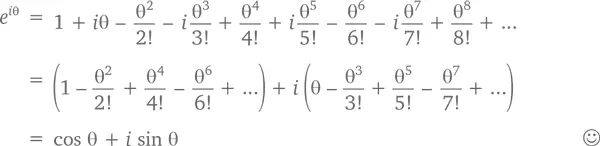
Это приводит нас к доказательству «уравнения Бога», с которого мы начинали эту главу. Приняв θ = π рад (или 180°), мы получим

Но это далеко не все, о чем говорит нам теорема Эйлера. Мы уже встречались с cos θ + i sin θ – это есть точка на единичной окружности, лежащей на комплексной плоскости. Вместе с «положительной» половиной оси x она образует угол θ. Так вот, с помощью теоремы Эйлера эту точку можно представить очень простым способом – таким, какой показан на графике

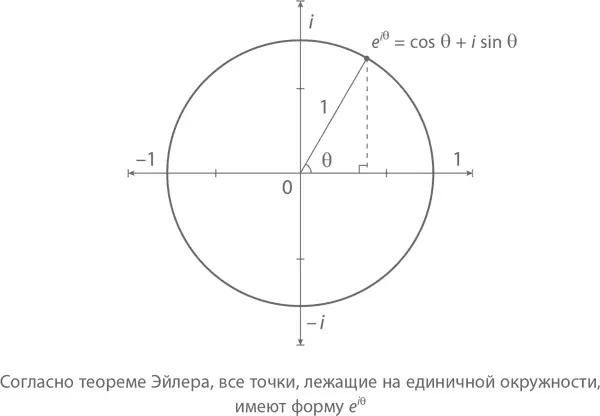
Но и это еще не все! Любая точка комплексной плоскости имеет на окружности свое соответствие. А именно комплексная величина z с модулем R и углом θ представляет собой некую в R раз увеличенную точку, лежащую на окружности. Другими словами,

Следовательно, если у нас на комплексной плоскости есть две точки z 1= R1e iθ 1 и z 2= R 2e iθ 2 , то, согласно правилам действий со степенями (в версии, касающейся комплексных величин)

что является комплексным числом с модулем R 1 R 2и углом θ 1+ θ 2. И снова мы приходим к выводу, что произведение комплексных величин – это, по сути, произведение их модулей и сумма их углов. Только согласитесь: теорема Эйлера и число e приводят нас к этому умозаключению куда безболезненнее и быстрее, чем наше предыдущее – длиной в целую страницу – алгебраическо-тригонометрическое доказательство.

Давайте же восславим число e уже ставшим привычным для нас способом (и да простит нас Джойс Килмер [35]):

Математика – это язык, на котором говорит наука. Стоит ли удивляться, что большинство законов природы описываются с помощью математического алфавита? Исчисление – один из способов познать суть вещей, то, как они изменяются, развиваются, движутся. Эту главу мы посвятим измерению скорости, с которой изменяются функции, и изучению теории приближений – примерной оценки (аппроксимации) сложных и простых полиномиальных функций (многочленов). А еще исчисление – мощное средство оптимизации . Это наиболее эффективный способ подобрать такие величины и порядок работы с ними, которые дадут оптимальный результат. (Например, если мы планируем доходы или надеемся выжать максимум при минимуме затраченных усилий, результат должен быть наибольшим, а если хотим сэкономить или ищем кратчайший путь из точки А в точку Б, – наименьшим.)

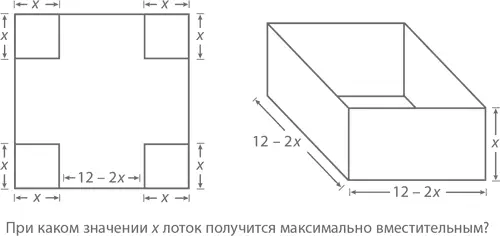
Предположим, что у вас есть лист картона размером 12 на 12 см (см. рисунок). Наша задача – сделать из него лоток, для чего нам нужно от каждого из четырех углов отрезать по квадратику размером x на x сантиметров. Чему должен быть равен x , чтобы у нас получился максимально вместительный лоток?

Представим объем как функцию x . Площадь основания лотка равна (12 – 2 x )(12 – 2 x ), а высота его стенок – x . Значит, объем можно посчитать как

кубических сантиметров. Значение x должно быть таким, чтобы значение V было максимальным. Однако в крайности впадать не следует: при x = 0 или x = 6 объем лотка будет нулевым. Значит, оптимальный результат лежит где-то между этими двумя значениями.

Попробуем графический подход – визуализируем функцию y = (12 – 2 x )² x для значений x в диапазоне от 1 до 6. При x = 1 объем составит y = 100; при x = 2 – y = 128; при x = 3 – y = 108. Значение x = 2 выглядит многообещающе, но что, если в диапазоне от 1 до 3 есть другая действительная величина, которая подойдет нам еще лучше?

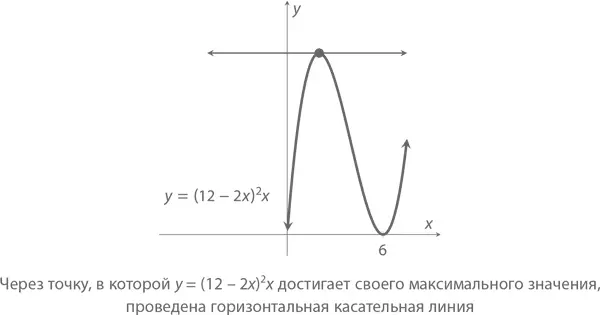
Влево от максимума функция растет, вправо – уменьшается. Слева значение ее наклона положительное, справа – отрицательное. В самой верхней точке не происходит ничего – функция в ней словно застыла в нерешительности, выбирая, куда направиться: вверх или все-таки вниз. Поэтому через нее можно смело провести горизонтальную (то есть с нулевым наклоном) касательную. Именно ее – такую оптимальную точку – мы и будем искать в этой главе.