Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Теорема:Если y = e x , то y' = e x .

Почему f ( x ) = e xсоответствует f '( x ) = e x? Смотрите, в чем секрет. Сначала обратите внимание на то, что

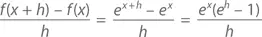
Вспомним, что е , по сути, есть

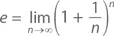
что означает, что с увеличением n значение члена (1 + 1/ n ) nбудет все ближе и ближе подходить к e . Теперь предположим, что h = 1/ n . При очень большом значении n h = 1/ n находится очень близко к 0. Следовательно, при h , близком к 0,

Возведя обе части в степень h (и помня, что ( a b ) c = a bc ), получаем

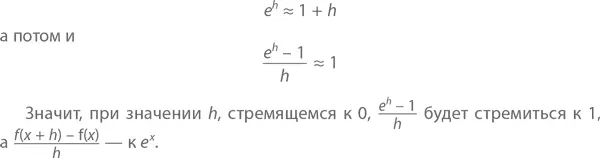
А есть ли еще такие функции, которые равны своим производным? Есть. Но все они сводятся к y = ce x , где c заменяется любым действительным числом (в том числе и 0, который превращает функцию в постоянную y = 0).

Не так давно мы выяснили, что при сложении функций производная суммы равна сумме производных. А что насчет умножения? Увы, но производная произведения не равна произведению производных. Тем не менее посчитать ее не очень сложно – для этого достаточно воспользоваться несложной теоремой.

Теорема (правило дифференцирования произведения функций):Если y = f ( x ) g ( x ), то

Например, согласно правилу дифференцирования произведения, чтобы продифференцировать y = x 3 e x , нам нужно взять f ( x ) = x ³ и g ( x ) = ex . В результате у нас получится

Обратите внимание, что при f ( x ) = x 3и g ( x ) = x 5их произведение, согласно тому же правилу, составит x 3 x 5= x 8. Производная же будет выглядеть как

что полностью соответствует правилу дифференцирования степенной функции.

Доказательство (правило дифференцирования произведения функций):Предположим, что u ( x ) = f ( x ) g ( x ). Тогда

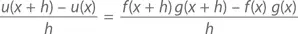
А дальше творим истинно математическое волшебство – добавляем к числителю 0, но не привычным способом, а с помощью прибавления и вычитания f ( x + h ) g ( x ):

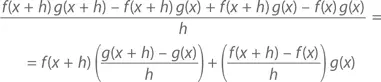
Так как h → 0, в результате имеем f ( x ) g' ( x ) + f' ( x ) g ( x ), что и требовалось доказать.◻

Но доказанное правило полезно не только в этом конкретном случае – с его помощью можно найти производные других функций. Мы уже доказали, что правило дифференцирования степенной функции верно при положительных значениях показателя степени. Давайте посмотрим, как оно поведет себя при дробных и отрицательных значениях.

Например, согласно правилу дифференцирования степенной функции

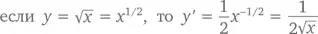
Сможем ли мы доказать его с помощью правила дифференцирования произведения? Предположим u ( x ) = √ x . Тогда

Продифференцировав обе стороны и применив правило дифференцирования произведения, получаем

Следовательно, 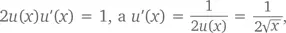как мы и предполагали.

Правило дифференцирования произведения при отрицательных значениях степени гласит, что y = x −n будет иметь производную 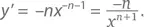Чтобы это доказать, возьмем u ( x ) = x −n , где n ≥ 1. Согласно определению, при x ≠ 0

Продифференцировав обе стороны и применив правило дифференцирования произведения, получаем

Разделив всех члены уравнения на x n и перенеся первый член в другую часть уравнения, получаем

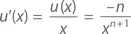
что и требовалось доказать.◻

Следовательно, если y = 1/ x = x –1, то y ' = −1/ x ², если y = 1/ x ² = x –2, то y ' = −2 x –3= −2/ x ³, и т. д.

Помните, в 7 главе мы искали такое положительное значение x , при котором функция

показала бы минимальное значение? Тогда мы нашли решение с помощью геометрии, показав, что результат может быть достигнут при x = 1. Но можно решить эту задачу значительно проще: это значит, что y ' = 0, это дает нам 1 – 1/ x ² = 0, а единственная положительная величина, которая удовлетворяет этому условию, – x = 1.

Что касается тригонометрических функций, то их дифференцировать ничуть не сложнее. Обратите внимание, что для доказательства следующей теоремы нам нужно, чтобы углы были выражены в радианах.