Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Обобщая, можно сказать, что при y = sin ( g ( x )) y' = g' ( x ) cos( g ( x )). Та же логика подсказывает нам, что y = cos ( g ( x )) имеет производную y' = – g' ( x ) sin ( g ( x )).

С другой стороны, функция y' = – g' ( x ) sin ( g ( x )), согласно цепному правилу, выглядит так:

Обобщим и это: цепное правило говорит нам, что при y = ( g ( x )) ny' = n ( g ( x )) n –1 g' ( x ). А что насчет y = ( x 3) 5?

что полностью соответствует правилу дифференцирования произведения функций.

Продифференцируем y = √( x2 + 1 ) = ( x² +1) ½ .

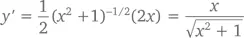
Со степенными функциями дело обстоит ничуть не сложнее. Так как ex является собственной производной, то при y = e g ( x )имеем

Например, производная y = e x³ – y' = (3 x² ) e x³ .

Обратите внимание, что функция y = e kx имеет производную y' = ke kx = ky . Это одна из причин, почему показательные (экспоненциальные) функции так важны – они появляются, когда скорость роста функции пропорциональна величине ее значения. По этой причине показательные функции часто связаны с процессами в финансовой сфере и в биологии.

Натуральный логарифм ln x обладает одним интересным свойством:

при любом значении x , большем 0. Чтобы найти его, логарифма, производную, воспользуемся цепным правилом. Допустив, что u ( x ) = ln x , получим e u ( x )= x . Продифференцировав обе части этого уравнения, получаем u' ( x ) e u ( x )= 1. Но поскольку e u(x)= x, u' ( x ) = 1/ x . Другими словами, если y = ln x, тогда y' = 1/ x . Вновь применив цепное правило, получаем: если y = ln ( g ( x )), то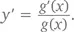

Давайте соберем все найденное с помощью цепного правила в таблицу:

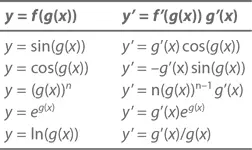
Хотите применить все это на практике? Вот вам задачка, практичней некуда. Корова Клара пасется в километре на север от реки (оси x ), в 3 километрах на запад и в километре на юг от коровника. Наевшись и нагулявшись, она решила попить водички и пойти домой. Естественно, ей хочется сделать это все как можно быстрее. Где именно ей нужно спуститься к реке, чтобы максимально сократить путь?

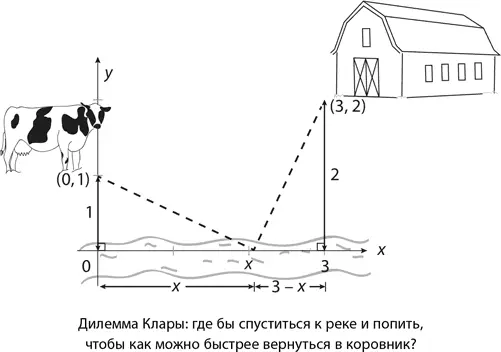
Предположим, что корова решила двинуться с луга (то есть из стартовой точки (0, 1)) к месту водопоя (то есть к точке ( x , 0)) напрямик. Согласно теореме Пифагора (или формуле расстояния), длина ее маршрута до реки составит √( x² + 1 ), а до амбара, находящегося в точке B = (3, 2), – √( (3 – x)² + 4 ) = √( x² – 6x + 13 ). Значит, задача сводится к нахождению такого значения x в диапазоне от 0 до 3, при котором достигается минимальное значение функции

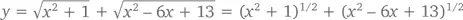
Продифференцировав это уравнение (с помощью цепного правила) и приравняв его к 0, получим

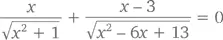
Проверить это можно, взяв x = 1, тогда левая часть уравнения превращается в 1/√ 2 – 2/√ 8 , что и в самом деле равно 0 (а можно добавить x /√( x² + 1 ) справа, возвести обе части в квадрат и умножить члены крест-накрест – после нескольких сокращений вы придете к x = 1).

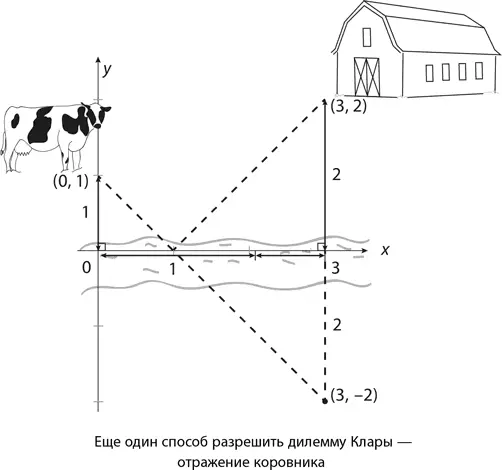
Неплохим вариантом будет метод отражения , уже знакомый нам по главе 7. Представьте, что вместо коровника (точка B = (3, 2)) корова пошла к его отражению (точка B' = (3,–2)), как показано на следующем рисунке.

Расстояние до B' абсолютно такое же, как и до B . Любой отрезок, соединяющий точку, расположенную на севере от реки, с ее «отражением», расположенным к югу от реки, неизбежно пересечет ось x . Кратчайшим маршрутом в этом случае будет прямая линия от (0, 1) до (3, –2) (с наклоном –3/3 = –1), пересекающая ось x при x = 1. И никаких квадратных корней!

Доказывая в конце прошлой главы уравнение Эйлера, мы воспользовались тремя загадочными формулами:

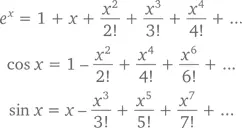
Перед тем как разбираться, как мы пришли к этому, давайте немного поиграем. Интересно, что получится, если взять отдельно каждый член ряда e x и продифференцировать? Правило дифференцирования степенной функции говорит нам, что производной функции x 4/4! будет (4 x 3)/4! = x 3/3! то есть предшествующий член ряда! Другими словами, продифференцировав ряд e x , мы вновь получим ряд e x , что полностью соответствует тому, что мы знаем о показательной функции e x !

Последовательно дифференцируя x – x 3/3! + x 5/5! – x 7/7! +…, получаем 1 – x 2/2! + x 4/4! – x 6/6! +…, что соотносится с тем, что производная синуса – это косинус. Справедливо и обратное: производная косинуса – это синус со знаком минус. А еще этот ряд лишний раз доказывает, что cos 0 = 1, и поскольку каждая степень в нем выражена четным числом, значение cos (– x ) будет равно cos x . Впрочем, нам это уже известно (например, (– x ) 4/4! = x 4/4!). Следуя той же логике, мы можем прийти к sin 0 = 0, а поскольку каждая степень выражена нечетным числом, sin (– x ) = –sin x , как мы и предполагали.