Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Теорема:Если y = sin x , то y ' = cos x , а если y = cos x , то y ' = –sin x . Другими словами, производная синуса равна косинусу , а производная косинуса – синусу со знаком минус .

Доказательство:Для доказательства нам потребуется следующая лемма ( лемма – это подсобная, подготовительная теорема, с помощью которой можно доказать более сложное и серьезное утверждение).

Лемма:

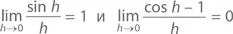
Здесь утверждается, что значение любого угла h , равного чуть больше, чем 0 (в радианах), будет близко к значению h , в то время как значение косинуса будет близко к 1. С помощью калькулятора, например, можно выяснить, что sin 0,0123 = 0,0122996…, а cos 0,0123 = 0,9999243…. С помощью этой леммы можно продифференцировать любой синус или косинус. Тождество sin ( A + B ) из главы 9 говорит нам, что

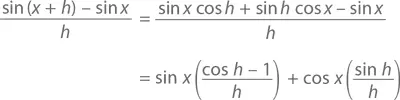
А так как h → 0, то, согласно нашей лемме, это уравнение превращается в (sin x )(0) + (cos x )(1) = cos x . Подобным же образом

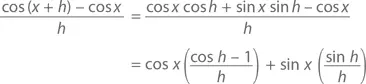
И снова h → 0 дает нам (cos x )(0) – (sin x )(1) = –sin x , что и требовалось доказать.◻

То, что можно доказать с помощью такого вот графика:

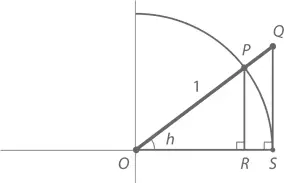
На единичной окружности, часть которой изображена выше, R = (1, 0), а P = (cos h , sin h ), где h есть небольшой угол с положительным значением. В прямоугольном треугольнике OQR

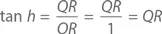
Рассмотрим сектор OPR , имеющий клинообразную форму. Площадь единичной окружности равна π1² = π, сектор OPS – ее часть, выражаемая дробью h /(2π). Следовательно, площадь сектора OPR составляет π( h /2π) = h /2.

Так как сектор OPR содержит в себе треугольник OPS , а тот, в свою очередь, – треугольник OQR , сравнение их площадей дает нам

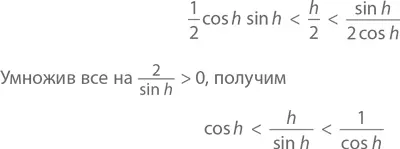
Для положительных значений a, b и c , если a < b < c , то 1/ c < 1/ b < 1/ a . Следовательно,

А так как h → 0, и cos h , и 1/cos h будут стремиться к 1, что и требовалось доказать.

◻

С помощью полученного результата и нескольких алгебраических формул (включая cos² h + sin² h = 1) можно доказать, что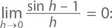

◻

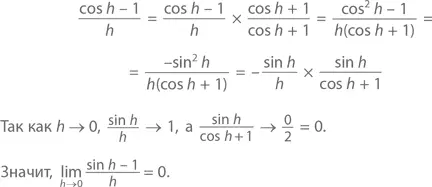
Производные синуса и косинуса – ключи к дифференцированию тангенса.

Теорема:Если y = tan x , то y' = 1/(cos² x ) = sec² x .

Доказательство:Предположим, что u ( x ) = tan x = (sin x )/(cos x ). Тогда

Продифференцировав обе части и применив правило дифференцирования произведения функций, получим

Разделим все члены на cos x и решим уравнение для tan ' ( x ):

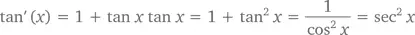
в котором предпоследнее значение получается в результате деления тождества cos 2 x + sin 2 x = 1 на cos 2 x .

Доказательство правила дифференцирования частного:Так как u ( x ) g ( x ) = f ( x ), продифференцировав обе части уравнения, в соответствии с правилом дифференцирования произведения получим

Умножив все на g ( x ), получим

Заменим g ( x ) u ( x ) на f ( x ) и решим уравнение для u' ( x ), что приведет нас к искомому результату.◻

Теперь мы умеем дифференцировать многочлены, показательные и тригонометрические функции. Также мы научились дифференцировать их суммы, произведения и частные. Но есть еще сложные функции – функции от функций, с которыми тоже нужно уметь обращаться. Правило дифференцирования сложной функции иначе называют цепным правилом. Согласно ему, например, если f ( x ) = sin x , а g ( x ) = x ³, то

Не перепутайте: это не то же самое, что

Теорема (цепное правило):Если y = f ( g ( x )), то y' = f' ( g ( x )) g' ( x ).

Например, если f ( x ) = sin x , а g ( x ) = x ³, то f' ( x ) = cos x , а g' ( x ) = 3 x ². Согласно цепному правилу, при y = f ( g ( x )) = sin ( x ³)