Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

А заодно мы коснемся касательных, и для этого нам придется среза́ть углы, причем не только в переносном, но и вполне себе прямом (как мы это делали только что в задачке про лоток) смысле.

Исчисление – штука непростая и громоздкая: у вас вряд ли получится найти по ней учебник меньше, чем на тысячу страниц. В нашем же распоряжении их едва ли больше 20, поэтому единственное, что мы успеем – так это чуть-чуть посветить спичкой в темной комнате. Все, что нам предстоит увидеть, – дифференциальный аспект исчисления, касающийся функций; интегральную же сторону, необходимую для того, чтобы подсчитывать площади и объемы сложных объектов, придется оставить пылиться в углу.

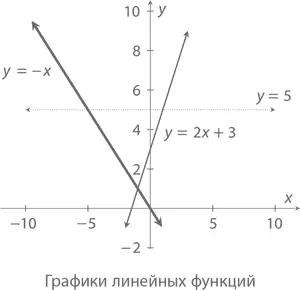
Начнем с самого простого – функций, представленных прямыми. В главе 2 мы уже говорили о том, что наклон графика линейной функции y = mx + b равен m . Следовательно, при росте значения x на единицу y будет увеличиваться на m . Допустим, наклон y = 2 x + 3 равен 2. Увеличив x на 1 (скажем, с x = 10 до x = 11), мы тем самым увеличим y на 2 (то есть с 23 до 25).

На графике ниже проведено несколько разных линий. Диагональная функция y = – x имеет наклон –1, а горизонтальная y = 5 – наклон 0.

Задав две точки, мы можем провести через них прямую. Ее наклон можно определить, не прибегая к формуле самой прямой, – достаточно взять координаты точек ( x 1, y 1) и ( x 2, y 2) и вставить их в уравнение

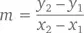
позволяющее узнать отношение приращения функции к приращению аргумента.

Для примера возьмем линию y = 2 x + 3 и две ее точки с координатами (0, 3) и (4, 11). Ее наклон составит 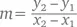= (11 – 3)/(4 – 0) = 8/4 = 2 – тот же ответ, к которому мы можем прийти с помощью уравнения прямой.

Теперь рассмотрим функцию y = x ² + 1, изображенную на графике внизу. Это не прямая: мы можем проследить, как постоянно меняется ее наклон. А вот касательная, проходящая через точку (1, 2) – прямая. Попробуем определить ее наклон.

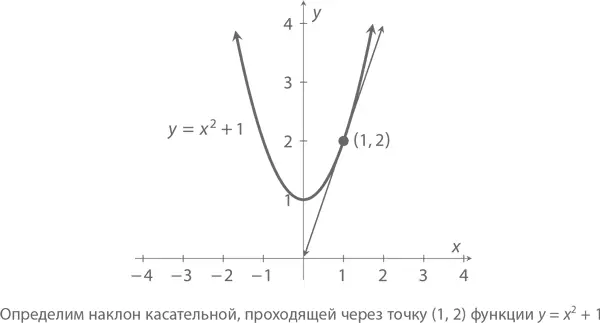
Для этого нам нужны хотя бы две точки. Что же делать? Придется взять еще одну линию – такую, которая пересекает кривую функции как минимум дважды (так называемую секущую ). Приняв x = 1,5, мы получаем y = (1,5)² + 1 = 3,25. Согласно уже рассмотренной нами формуле, наклон секущей составляет

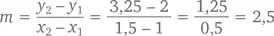
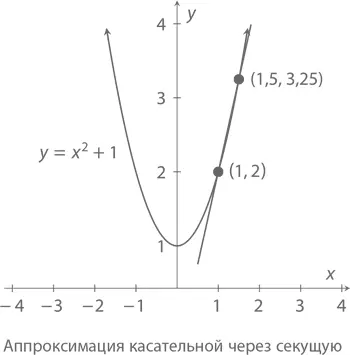
Для более точного результата переместим вторую точку как можно ближе к (1, 2). Скажем, если x = 1,1, то y = (1,1)² + 1 = 2,21, а наклон секущей – m = (2,21 – 2)/(1,1 – 1) = 2,1. Посмотрите на таблицу: при постепенном приближении второй точки к (1, 2), наклон секущей будет столь же постепенно приближаться к 2.

Посмотрим, что происходит, когда x = 1 + h (при h ≠ 0), но лишь чуть-чуть отличается от x = 1. Тогда y = (1 + h )² + 1 = 2 + 2 h + h ², а наклон секущей составит

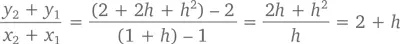
То есть при приближении h к 0 наклон графика функции будет приближаться к 2. В записи это выглядит так:

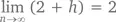
Подобным представлением мы хотим сказать, что предел 2 + h при значении h , стремящемся к 0, равен 2. Так мы и узнаем наклон касательной к кривой y = x ² + 1 в точке (1, 2) – 2.

А вот как все это выглядит в обобщенном виде. Нам нужно найти наклон касательной к кривой y = f ( x ) в точке ( x, f ( x )). Как видно на графике, наклон секущей, проходящей через точку ( x, f ( x )) и соседнюю с ней ( x + h, f ( x + h )), составляет

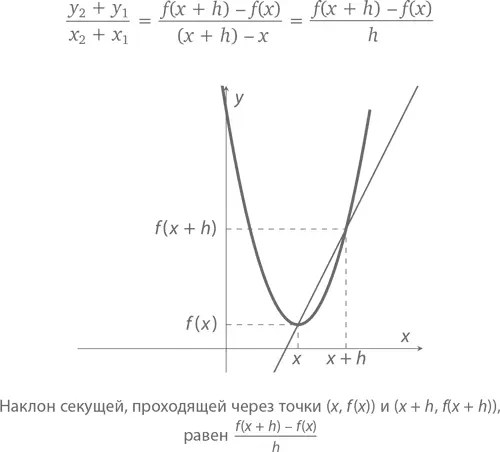
Представим наклон касательной, проходящей через точку ( x, f ( x )), как f ′( x ):

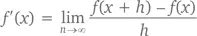
Выглядит не очень-то понятно, поэтому давайте возьмем парочку более конкретных примеров. Для прямой линии y = mx + b , а f ( x ) = mx + b . Чтобы найти f ( x + h ), нужно заменить x на x + h – это позволит нам подсчитать f ( x + h ) = m ( x + h ) + b . Следовательно, наклон секущей равен

Наклон касательной будет равен m при любом значении x , поэтому f ′( x ) = m . Объясняется это тем, что линия y = mx + b всегда имеет наклон m .

Обратимся к производной функции y = x ². Согласно только что сформулированному определению,

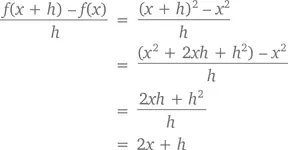
а так как h стремится к 0, f ′( x ) должно быть равно 2 x .

При f ( x ) = x ³ получаем

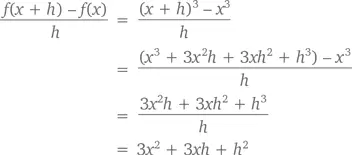
а так как h стремится к 0, f ′( x ) должно быть равно 3 x ².

Поиск производной функции f ′( x ) на основании функции y = f ( x ) называется дифференцированием . Впрочем, все не так сложно, как кажется: потренировавшись как следует и найдя производные нескольких простых функций, мы легко сможем определить их и для сложных функций. И, что самое приятное, никаких пределов! А вот и подходящая теорема.

Теорема:Если u ( x ) = f ( x ) + g ( x ), то u ′( x ) = f ′( x ) + g ′( x ). Другими словами, производная суммы есть сумма производных . Также если с – действительное число, производная cf ( x ) равна cf ′( x ).

Как следствие, мы можем утверждать, что, поскольку y = x ³ имеет производную 3 x ², а y = x ² – производную 2 x , производная y = x ³ + x ² будет равна 3 x ² + 2 x (например, производная функции y = 10 x ³ – 30 x ²).