Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Доказательство:Предположим, что u ( x ) = f ( x ) + g ( x ). Тогда

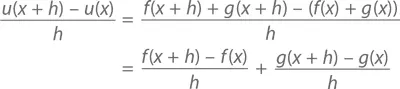
Положив h → 0 в качестве предела для обеих частей этого уравнения, получим

Обратите внимание, что, применяя этот предел справа, мы исходим из предположения, что предел суммы равен сумме пределов. Доказывать это мы, пожалуй, не станем – просто доверимся здравому смыслу, говорящему, что при приближении значений a и b к A и B значение a + b будет приближаться к A + B . Та же логика подсказывает нам, что предел произведения равен произведению пределов, а предел частного равен частному пределов. Но то, что справедливо для пределов, необязательно будет справедливо для производных. Например, производная произведения не равна произведению производных.

Что же касается второго утверждения нашей теоремы, то при v ( x ) = cf ( x )

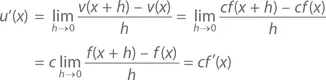
что и требовалось доказать.◻

Чтобы продифференцировать функцию f ( x ) = x 4, сначала распишем ее в следующем виде: f ( x + h ) = ( x + h ) 4= x 4+ 4 x ³ h + 6 x ² h ² + 4 xh ³ + h 4. Коэффициенты выглядят знакомо, правда? 1, 4, 6, 4, 1… Это же числа из 4 ряда треугольника Паскаля (см. главу 4)! Следовательно,

а так как h → 0, получается, что f ′( x ) = 4 x ³. Видите закономерность? Производные x, x ², x ³ и x 4равны 1, 2 x , 3 x ² и 4 x ³ соответственно. Применение того же алгоритма к бо́льшим степеням приводит нас к одному важному правилу. (Кстати, другое популярное обозначение производной – y ′. Так и будем писать.)

Теорема (правило дифференцирования степенной функции):При n ≥ 0

Например,

а

С помощью этого закона можно дифференцировать даже функции-константы, вроде y = 1, потому что 1 = x 0, а y = x 0имеет производную 0 x –1= 0 при любом значении x . Это объясняется тем, что линия y = 1 является горизонтальной. Исходя из правила дифференцирования степенной функции и предыдущей теоремы, мы сможем дифференцировать любой многочлен. Например, если

то

Правило дифференцирования степенной функции верно и при отрицательных значениях n . Например, если

Аналогичным образом, если

Жаль только, что доказать это нам пока что не по силам.

Перед тем как дифференцировать более сложные функции, применим уже полученные знания в не менее интересных и полезных целях. Например, в целях оптимизации.

Дифференциация нужна для того, чтобы выяснять, где функция достигает своего максимума, а где – минимума. При каком, например, значении x парабола y = x ² – 8 x + 10 достигает своей низшей точки?

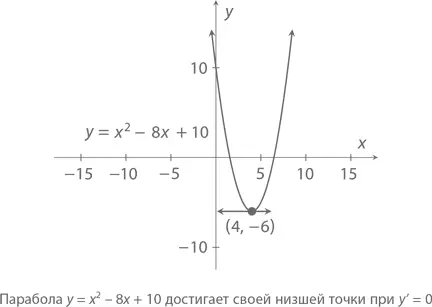
Как вы, наверняка, помните, проведенная через нее касательная должна иметь наклон 0. Так как y' = 2 x – 8, уравнение 2 x – 8 = 0 приведет нас к минимуму при x = 4 (кстати, y = 16 – 32 + 10 = –6). Для y = f ( x ) значение x , удовлетворяющее f' ( x ) = 0, называется критической точкой функции f . Функция y = x ² – 8 x + 10, например, имеет только одну критическую точку – x = 4.

Где же максимум? В нашем примере его попросту нет: значение y -координаты для x ² – 8 x + 10 может быть сколь угодно большим. Ограничить его можно одним единственным способом – определив для x пределы значений. Возьмем для примера 0 ≤ x ≤ 6. Тогда при x = 0 y будет равен 10, а при x = 6 – −2, то есть критической точкой для этой функции является x = 0. Обобщение этого приводит нас к одной очень важной теореме.

Теорема (теорема об экстремуме функции в точке):Если дифференцируемая на отрезке функция y = f ( x ) принимает максимальное или минимальное значение в точке x *, то x * должна быть либо критической точкой f , либо граничной точкой отрезка.

Давайте на секунду вернемся в начало главы, к задаче с лотком. Нам нужно, по сути, максимизировать функцию

где x должен находиться в диапазоне от 0 до 6. Нам нужно найти такой x , при котором значение y будет наибольшим. Так как наша функция представляет собой многочлен, ее производную можно найти как

Следовательно, ее критическими точками будут x = 2 и x = 6.

А так как мы знаем, что при объеме, равном 0, и конечных точках, равных 0 и 6, объем будет минимальным, нам остается только одна критическая точка – x = 2. Именно она и даст нам максимум – y = 128 см³.

Чем больше функций мы продифференцируем, тем больше задач сможем решить. Пожалуй, самой важной функцией в исчислении является показательная функция y = e x . Ее особенность в том, что она равна собственной производной.