Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Вмешивается e и в вопросы вероятности. Предположим, что раз в неделю вы покупаете лотерейный билет с шансом выиграть приз 1 к 100. Какова вероятность того, что за 100 недель вы что-нибудь да выиграете? Каждую неделю ваш «коэффициент удачи» равен 1/100 = 0,01, а «коэффициент невезения» – 99/100 = 0,99. Так как количество билетов неограниченно (то есть удача на этой неделе никак не зависит от невезения на прошлой), за весь срок получаем

что очень близко

Нет, это не совпадение. Вспомните формулу, в которой мы впервые увидели e x :

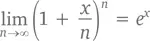
Если мы положим x = –1, то при любом большом значении n получим

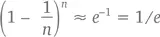
Когда n = 100, (0,99) 100будет примерно равно 1/ e . То есть ваши шансы выиграть приз за 100 недель составляют 1 – (1/ e ) ≈ 64 %.

Одна из самых моих любимых задач, связанных с вероятностью, – задача о сочетании пар . Представьте себе класс, состоящий из n учеников. Учитель раздает им тетрадки с проверенным домашним заданием. Но то ли по рассеянности, то ли от усталости раздает он их как попало, в случайном порядке (то есть тетрадка может попасть как к своему хозяину, так и к любому другому ученику). Каков шанс того, что ни одна из тетрадок не попадет в «правильные» руки? Иными словами, если мы возьмем все числа от 1 до n и «перемешаем» их в произвольном порядке, какова вероятность того, что ни одно из них не совпадет со своей «правильной» позицией? Например, при n = 3 чи́сла 1, 2 и 3 можно «перемешать» 3! = 6 разными способами, но под наши условия подходят только два из них: 231 и 312. Следовательно, для n = 3 нужная нам вероятность составит 2 к 6 или 1 к 3.

С количеством тетрадей, равным n , существует n ! возможных способов распределения их между учениками. Количество тех из них, которые соответствуют нашим условиям, обозначим как D n . Тогда шанс того, что никто из учеников не получит свою тетрадку, составит p n = D n / n !. Если n равно 4, то D nбудет равно 9:

И тогда p 4= D 4/4! = 9/24 = 0,375.

А вот каковы вероятности для других значений n :

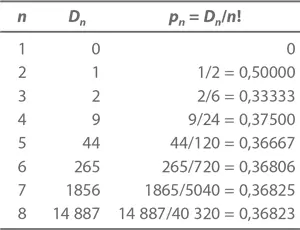
С увеличением n значение pn будет все ближе и ближе подбираться к 1/ e . И вот что самое удивительное: вероятность попадания тетрадок в руки их законных хозяев совершенно не зависит от количества учеников в классе, будь их десять, сто или миллион. И вероятность эта эти очень-очень близка к величине 1/ e .

Но откуда берется это 1/ e ? В первом нашем представлении, с числом учеников, равным n , возможность каждого из них получить свою тетрадь составляет 1/ n , а возможность получить чужую – 1 – (1/ n ). Возьмем последнюю величину и распространим ее на весь класс:

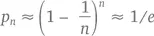
Почему приблизительно, спросите вы? Да потому что здесь, в отличие от задачи с лотерейными билетами, мы не сталкиваемся с последовательностью независимых друг от друга событий. Количество тетрадок ограничено, поэтому первое же «попадание» учителя в цель немного увеличит шансы второго ученика получить чужую тетрадку (то есть вместо 1/ n мы будем иметь уже 1/( n – 1)), а первый же «промах» – немного уменьшит. Но так как и в том и в другом случае вероятность изменяется незначительно, на верности нашего представления это не слишком сказывается.

Точное же значение p n основывается на бесконечной последовательности для e x :

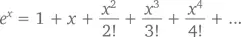
Если в этом уравнении мы подставим x = –1, у нас получится

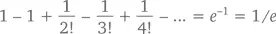
То есть в классе, состоящем из n учеников, вероятность того, что никто из них не получит свою тетрадь, составляет ровно

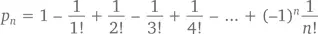
Например, если n = 4, p n= 1 – 1 + 1/2 – 1/6 + 1/24 = 9/24 – ответ, к которому мы уже приходили выше. Приближение к 1/ e здесь невероятно стремительно. Промежуток между p nи 1/ e меньше, чем 1/( n + 1)!. Следовательно, значение p 4находится в диапазоне от 1/5! = 0,0083 до 1/ e , значение p 10совпадает с 1/ e вплоть до 7 знаков после запятой, а значение p 100 – вплоть до 150 знаков!

Теорема:Число e является иррациональным.

Доказательство:Предположим обратное – что число e является рациональным. Тогда при положительных целых значениях m и n будет верно то, что e = m / n . С помощью n разобьем бесконечную последовательность для e на две части – так, чтобы e было равно L + R , то есть

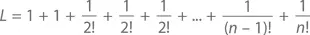
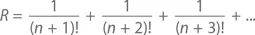
Обратите внимание, что n!e = en ( n– 1)! = m ( n– 1)! должно быть целой величиной (потому что и m , и ( n – 1)! суть целые величины), равно как и n!L (потому что n !/ k ! есть целая величина при любом k ≤ n ). Следовательно, n!R = n!e – n!L представляет собой разность двух целых чисел, а значит, и само является целым числом, что невозможно: поскольку условие, что n ≥ 1, означает, что

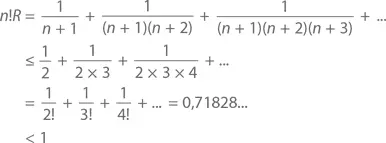
Не существует целых величин меньше 1, поэтому мы не можем считать n!R целым числом. Значит, наше предположение, что e = m / n , ведет к противоречию, из чего следует, что число e – иррациональное.◻

Число e было открыто и введено в оборот великим математиком Леонардом Эйлером. И именно Эйлер впервые обозначил его буквой e . Но, как полагает большинство специалистов по истории математики, вовсе не потому, что это была первая буква его фамилии [34]. Тем не менее e до сих пор достаточно часто называют «числом Эйлера».

Нам уже встречались бесконечные последовательности для функций e x , cos x и sin x . Откуда они берутся, мы узнаем в следующей главе. Сейчас же просто соберем их в одном месте: