Сергей Федин - Математики тоже шутят

В продолжение предыдущей темы стоит упомянуть про рефлексивные парадоксы.

В уже упоминавшейся ранее книге Дж. Литлвуда «Математическая смесь» справедливо говорится, что «все рефлексивные парадоксы являются, конечно, превосходными шутками». Там же приводятся два из них, которые я позволю себе процитировать:

1. Должны существовать (положительные) целые числа, которые не могут быть заданы фразами, состоящими менее, чем из шестнадцати слов. Любое множество положительных целых чисел содержит наименьшее число, и поэтому существует число N , «наименьшее целое число, которое не может быть задано фразой, состоящей из менее, чем шестнадцати слов». Но эта фраза содержит 15 слов и определяет N .

2. В журнале Spectator был объявлен конкурс на тему «Что бы Вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?» Первый приз получил ответ:

Первый приз во втором конкурсе этого года присужден мистеру Артуру Робинсону, остроумный ответ которого без натяжки должен быть признан наилучшим. Его ответ на вопрос: «Что бы Вы с наибольшим удовольствием прочли, раскрыв утреннюю газету?» был озаглавлен «Наш второй конкурс», но из-за лимитирования бумаги мы не можем напечатать его полностью.

Есть такие удивительные фразы, которые читаются одинаково и слева направо и справа налево. Одну наверняка знают все: А роза упала на лапу Азора . Именно ее просила написать в диктанте неуча Буратино капризная Мальвина. Называются такие взаимообратные фразы палиндромами, что в переводе с греческого означает «бегущий назад, возвращающийся». Вот еще несколько примеров: 1. Лилипут сома на мосту пилил . 2. Лезу на санузел . 3. Лег на храм, и дивен и невидим архангел . 4. Нажал кабан на баклажан . 5. Муза, ранясь шилом опыта, ты помолишься на разум . (Д. Авалиани). 6. Уж редко рукою окурок держу ... (Б. Гольдштейн) 7. Учуя молоко, я около мяучу . (Г. Лукомников). 8. Он верба, но она — бревно . (С. Ф.)

А интересно, есть ли палиндромы в математике? Для ответа на этот вопрос попробуем перенести идею взаимообратного, симметричного прочтения на числа и формулы. Оказывается, это не так уж и трудно. Познакомимся лишь с несколькими характерными примерами из этой палиндромной математики, палиндроматики . Оставляя в стороне палиндромные числа — например, 1991 , 666 и т.д. — обратимся сразу к симметричным формулам.

Попытаемся для начала решить такую задачу: найти все пары таких двузначных чисел

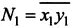
( x 1 — первая цифра, y 1 — вторая цифра) и

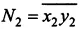
чтобы результат их сложения не менялся в результате прочтения суммы справа налево, т.е.

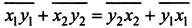
Например, 42 + 35 = 53 + 24.

Задача решается тривиально: сумма первых цифр у всех таких пар чисел равна сумме их вторых цифр . Теперь можно без труда строить подобные примеры: 76 + 34 = 43 + 67, 25 + 63 = 36 + 52 и так далее.

Можно развивать эти идеи дальше — например, так: 79 + 42 = 121 = 24 + 97 (Г. Лукомников) или даже так: XI + IV = VI + IX (В. Силиванов)

Рассуждая аналогичным образом, можно легко решить такую же задачу для остальных арифметических действий.

В случае разности, т.е.

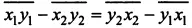
получаются следующие примеры: 41 – 32 = 23 –14, 46 – 28 = 82 – 64, ... — суммы цифр у таких чисел равны ( x 1 + y 1 = x 2 + y 2 ).

В случае умножения имеем: 63 ∙ 48 = 84 ∙ 36, 82 ∙ 14 = 41 ∙ 28, ... — при этом произведение первых цифр у чисел N 1 и N 2 равно произведению их вторых цифр ( x 1 ∙ x 2 = y 1 ∙ y 2 ).

Наконец, для деления получаем такие примеры:

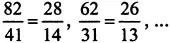
— в этом случае произведение первой цифры числа N 1 на вторую цифру числа N 2 равно произведению двух других их цифр, т.е. x 1 ∙ y 2 = x 2 ∙ y 1 .

Доказательство следующей «теоремы», появившейся в эпоху «недоразвитого социализма», опирается на популярные тезисы тех лет относительно роли Коммунистической партии.

Теорема. Роль партии — отрицательна.

Доказательство. Хорошо известно, что:

1. Роль партии непрерывно возрастает.

2. При коммунизме, в бесклассовом обществе, роль партии будет нулевой.

Таким образом, имеем непрерывно возрастающую функцию, стремящуюся к 0. Следовательно, она отрицательна. Теорема доказана.

Несмотря на кажущуюся абсурдность следующей задачи, у нее, тем не менее, есть вполне строгое решение.

Задача.Мама старше сына на 21 год. Через шесть лет она будет старше его в пять раз. Спрашивается: ГДЕ ПАПА?!

Решение. Пусть X — возраст сына, а Y — возраст мамы. Тогда условие задачи записывается в виде системы двух простых уравнений:

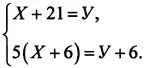
Подставляя Y = X + 21 во второе уравнение, получим 5 X + 30 = X + 21 + 6, откуда X = –3/4. Таким образом, сейчас сыну минус 3/4 года, т.е. минус 9 месяцев. А это значит, что папа в данный момент находится на маме!

Хорошо известно ироническое выражение «Если ты такой умный, то почему ты такой бедный?», применимое, увы, очень ко многим. Оказывается, у этого грустного феномена есть строгое математическое обоснование, опирающееся на столь же бесспорные истины.

А именно, начнем с двух всем известных постулатов:

Постулат 1: Знание = Сила.

Постулат 2: Время = Деньги.

Кроме того, любой школьник знает, что

Путь s = Скорость x Время = Работа : Сила ,

Откуда

Работа : Время = Сила x Скорость (*)

Подставляя значения для «времени» и «силы» из обоих постулатов в (*), получим:

Работа : (Знание x Скорость) = Деньги (**)

Из полученного равенства (**) видно, что устремляя «знание» или «скорость» к нулю, мы можем получить за любую «работу» сколь угодно большие деньги.

Отсюда вывод: чем глупее и ленивее человек, тем больше денег он сможет заработать.