Филип Болл - Музыкальный инстинкт. Почему мы любим музыку

Рис. 6.20 Модуляции без вступлений в музыке Прокофьева: Соната для фортепиано № 5 (а) и вальс из балета «Золушка» (б).

Какими бы смелыми ни были траектории в гармоническом пространстве, они не могут быть произвольнее движений в мелодическом пространстве. Все, кто вырос в диатонической тональной традиции, а значит, фанаты и Майкла Джексона, и Майкла Типпета, нуждаются в логике модуляции, чтобы та была доступна для восприятия. Можно выдумать новые пути, но они все равно должны куда-либо вести; нам необходимо понимание образа гармонического пространства.

Таким же образом, как теоретики музыки и психологи пытались нарисовать принцип отношений между нотами в диатонической и хроматической гаммах, они попытались создать карты аккордов и тональностей. Первые опыты в картографии такого рода основывались на музыкальной теории, то есть на отношениях между тоническим трезвучием и различными трезвучиями мажорной гаммы. Из этого мы можем заключить, что любой мажорный аккорд I в каком-то смысле «ближе» к двум другим мажорным аккордам (IV и V) и трем минорным (ii, iii и iv). Гармоническая прогрессия из тоники к любым из этих аккордов будет «звучать правильно», хотя и в неодинаковой степени (вскоре мы это увидим). Но у мажорного аккорда есть свой минор (i) – переход между мажором и минором тоже считается «допустимым» ходом и удивительно популярен в классической музыке, например, его можно услышать в известном «Rondo alla Turca» из Сонаты для фортепиано № 11, K331, а также в Сонате для фортепиано № 19, Op. 49 No. 1 и в Вальсе си ми минор Op. 69 No. 2 Шопена. А минорный аккорд связан с минорами v и iv, как параллельный мажор, закрепленный на минорном трезвучии (например, c-Eb).

Рис. 6.21 Двумерная репрезентация гармонического пространства. Сетка продолжается без ограничений.

Все это говорит о том, что единственная возможная репрезентация гармонического пространства тональностей, где родственные аккорды располагаются рядом на двумерной сетке, показана на рисунке 6.21. Арнольд Шенберг в 1954 году привел подобную карту в книге «Структурные функции гармонии». Движения по вертикали проходят по цепочке квинт, а по горизонтали мы переходим поочередно между мажором/минором и мажором/параллельным минором. Схема повторяется по вертикали (но смещается по горизонтали) через каждые три ряда. С учетом того, что при равномерной темперации фа-диез становиться эквивалентом соль-бемоль и так далее, повтор появляется по горизонтали в каждом восьмом столбце. Гармоническая вселенная замкнута сама на себя и имеет форму пончика или тора. Традиционные модуляции в теории музыки продвигаются маленькими шагами по сетке по вертикали, горизонтали или по диагонали.

Это все теория, но имеет ли какое-либо отношение такая карта к реальному восприятию гармонического пространства? Кэрол Крумгансл попыталась найти ответ и на этот вопрос. Один из способов оценки отношений между тональностями заключается в рассмотрении степени корреляции тональных иерархий (стр. 103) поочередно для каждой пары. Вспомните, что эти тональные иерархии отражают, насколько хорошо каждая нота хроматической гаммы подходит в определенный тональный контекст. Мы можем сравнить один график с другим и оценить, насколько они подходят друг к другу. Когда Крумгансл и Кесслер выполнили это действие, они обнаружили, что результат подтверждает музыкальную интуицию: чем дальше мы продвигаемся по цепочке квинт, тем менее родственными становятся две тональности, – до тех пор, пока мы не попадем на другую сторону, где сходство снова начинает возрастать (Рис. 6.22). Похожая схема верна и для минорных тональностей, только с той разницей, что U-образная форма корреляции искажена и на месте параллельного минора появляется бугорок, где степень перекрытия повышается.

Но гармоническое пространство устроено гораздо сложнее, поскольку в него вовлечены отношения не только между тоническим и другими аккордами, но и между всеми остальными аккордами. Стоит ли ближе аккорд ii (ре минор в тональности до) по ощущениям к аккорду IV (фа) или аккорду iv (ля минор)? На Рисунке 6.21 два последних соседствуют на одинаковом расстоянии, но как в действительности мы оцениваем их близкое расположение? Существует множество возможных пермутаций в отношениях, а потому гармоничное пространство становится многомерным. Представьте, что вы хотите нарисовать карту социальных связей с друзьями из соцсети. Джо и Мэри оба мои хорошие друзья, но при этом они никогда не встречались. Поэтому, если я помещу их на одинаковом расстоянии от себя, то они неизбежно окажутся близко друг к другу, из-за чего сложится ложное представление о близости их отношений. Как же нам изобразить пространство, чтобы учесть все подобные ситуации?

К счастью, когда Крумгансл и ее коллеги оценивали отношения с помощью метода «пробного тона» (или в данном случае «пробного аккорда»), они проигрывали испытуемым звукоряд для установления тонального контекста, следом играли два аккорда и просили оценить степень их совместимости с текущим контекстом – они обнаружили, что результаты можно вполне достойно изобразить на двумерной карте (Рис. 6.23). Можно сказать, что, как и в аналогии с соцсетью, два ваших близких друга, вероятно, знают друг друга, также если и два аккорда обнаруживают сильную связь с третьим, то они, скорее всего, близко связаны друг с другом – независимо от тонального контекста. Таким образом, многомерное пространство может быть без потерь сложено в двумерное и изображено на бумаге.

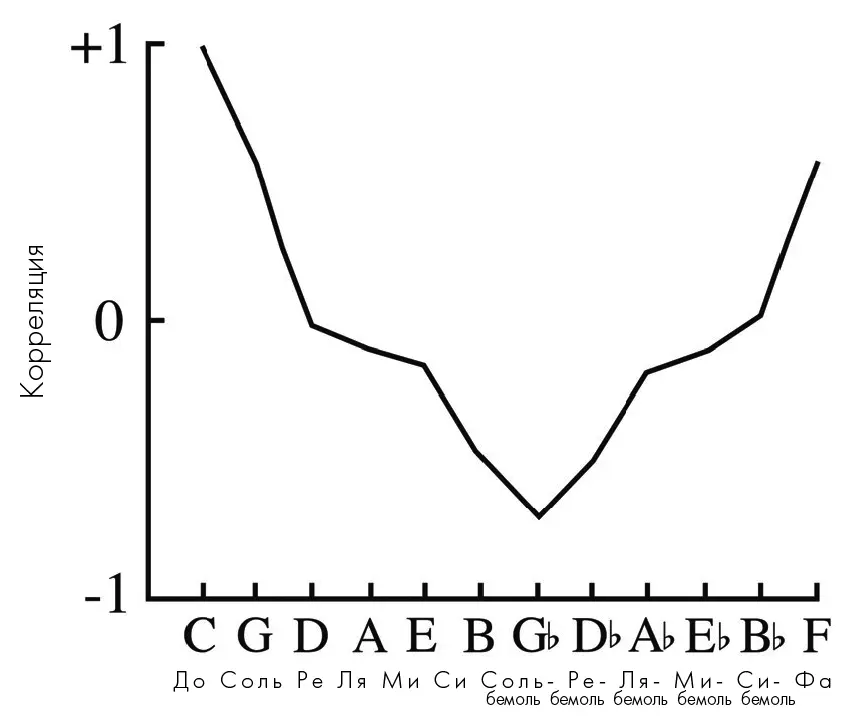
Рис. 6.22 Один из способов проверки «совместимости» тональностей заключается в оценке статистики корреляций их тональных иерархий (стр. 103). Здесь показаны результаты для до мажор в сравнении с другими мажорными тональностями, восходящими по цепочке квинт.

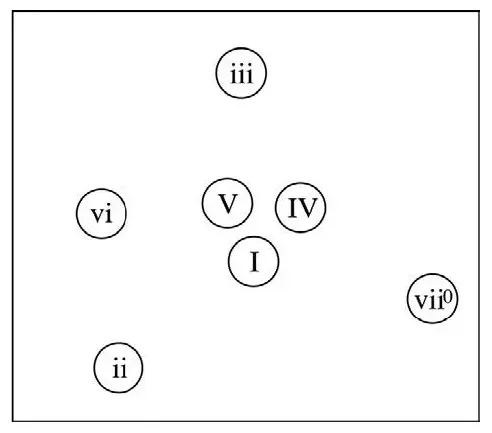
Рис. 6.23 Гармоническое пространство тонических аккордов, выведенное из экспериментов с «пробным тоном». Расстояния между аккордами совпадают со степенью их сходства с позиции восприятия.

В получившейся карте нет особо удивительных результатов: тонический, доминантовый и субдоминантовые аккорды стоят рядом, аккорды iii, vi и ii находятся примерно на одинаковом расстоянии от основного кластера, а уменьшенной аккорд vii0 оказался в отдалении. Теоретик музыки мог бы догадаться о таком расположении, но что определяет схему? Возможно, что-то связанное с количеством общих нот в аккордах или степенью их консонантности? Или же все дело в простой заученной ассоциации? Крумгансл и коллеги выяснили, что, как и в случае с тоновой иерархией, преобладает фактор обучения: существует прямая связь между суждением о сопоставимости и частотностью использования аккорда в классической музыке в соответствующей тональности в музыке восемнадцатого и девятнадцатого столетия (до 1875 года). Другими словами, чем чаще пользуются аккордами, тем лучше их кажущаяся совместимость. Было выявлено гораздо меньше совпадений с количеством сенсорного консонанса между соотвествующими аккордами. [46] Тестирование было далеко не идеальным. В действительности его можно серьезно рассматривать, если бы музыкальный опыт всех испытуемых был получен от прослушивания классической музыки указанного периода; было бы куда лучше посмотреть количество корреляций в той музыке, которую испытуемые слушают на самом деле. Но как мы уже убедились, гармонические традиции того периода классической музыки практически полностью заимствованы современной популярной музыкой.