Филип Болл - Музыкальный инстинкт. Почему мы любим музыку

Крумгансл исследовала этот вопрос путем экспериментов. Она задалась вопросом, какие ноты хроматической гаммы по ощущениям лучше всего вписываются в контекст, предложенный аккордом «Петрушка». Как вы думаете, слушатели выбрали диатонические гаммы до и фа-диез или октатонику? Ни то и ни другое! Тональная иерархия, полученная из этих тестов на восприятие, сильно совпадала со схемой, предложенной музыковедом Питером вад ден Турном. В соответствии с ней октатоновый набор нот разделен по принципу иерархии, как ноты мажорной гаммы: до и фа-диез здесь самые выдающиеся, за ними следуют группы (до-ми-соль) и (фа-диез – ля-диез – до-диез), а затем все восемь нот.

Это говорит о том, что слушатели в состоянии вникнуть в необычную гармонию методом, который не входит в основы традиционной западной теории музыки. Практически никто не знает о существовании экзотической октатоновой иерархии Турна, и все же слушатели подсознательно выделяют эту организационную структуру из самой музыки, – прямо сходу и из музыкального отрывка, который звучит всего несколько секунд! Стоит вспомнить, как слушатели устанавливали новые тональные иерархии, чтобы осмыслить незнакомые звукоряды других культур (стр. 106). И вновь мы убеждаемся в том, как мало формальной практики и теоретических знаний нужно для того, чтобы интерпретировать музыку и даже получать удовольствие от нового опыта.

Гармоническое пространство Крумгансл или нечто сходное представляется достойной репрезентацией ментальной карты, которой мы пользуемся для преодоления гармонической прогрессии, но это только примерный вариант, набросок одного из срезов многомерного пространства. Музыковед Дмитрий Тимочко из Принстонского университета вооружился музыкальной и математической теорией, чтобы представить более четкий и исчерпывающий план музыкального пространства: он исследовал формальные отношения между всеми возможными нотами и аккордами и результат получился почти пугающим, потому что такое извилистое многомерное пространство тяжело визуализировать и осмыслить даже математикам.

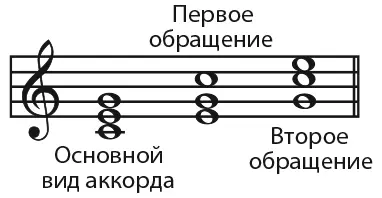
Рис. 6.29 Обращения трезвучия до мажор.

И все же в основе этой попытки лежит стремление к упрощению. Если мы представим все ноты фортепианной клавиатуры и все возможные варианты их сложений в музыкальные последовательности, секвенциальных или аккордовых, то получим астрономическое количество вариантов и никто не сможет понять это абстрактное пространство. Без таких музыкальных концепций, как гаммы, аккорды и тональности, мы бы просто пропали.

Эти концепции организовывают определенные группы нот в классы. Группы нот до-ми-соль и си-бемоль-ре-фа равнозначны в том смысле, что они представляют собой мажорные трезвучия; последняя может появиться из первой, если каждую ноту понизить на полтона. Таким же образом до-ми-соль равнозначна ми-соль-до и соль-до-ми, так как все они являются аккордами в до мажор, а два последних – обращения первого: у них одни и те же звуковысотные классы при различающейся нижней ноте (Рис. 6.29). До-ми-соль остается аккордом того же вида вне зависимости от октавы, на которой играется. Тимочко и его коллеги Клифтон Каллендер и Иен Куин занимались поисками способов геометрической репрезентации всех подобных эквивалентов, которые музыканты узнают в разных группах или последовательностях нот. Такие отношения можно описать математически как свойства симметрии: яблоко, отраженное в зеркале, все равно воспринимается как яблоко. После регистрации всех симметрий невозможное число способов организации нот в мелодии и аккордовые последовательности сокращается до гораздо более компактного подпространства. Это сравнимо с тем, как разные объекты отбрасывают одинаковую тень: через «проецирование» этих форм из трехмерного в двумерное пространство мы обнаруживаем симметрию, делающую их похожими друг на друга (Рис. 6.30); проекции в другие направления могут раскрыть другие наборы взаимосвязей.

Исследователи считают, что существует только пять распространенных типов трансформаций, применимых для определения эквивалентности в музыке, в том числе октавные сдвиги, перераспределения нот (например, обращения аккордов) и удвоения (например, прибавление высокой ми’ в аккорд до-ми-соль). Эквиваленты могут применяться сами по себе или в сочетаниях; например, существует тридцать два варианта, в которых два аккорда могут рассматриваться как «тождественные».

Симметрия «сворачивает» огромное пространство пермутаций нот определенными способами; в результате геометрические пространства остаются сложными, но теперь их можно подвергать математическому анализу и воспринимать интуитивно. В этих свернутых пространствах классы эквивалентных музыкальных объектов – например, трехнотные аккорды или мелодии из трех нот – могут быть представлены в виде точки. Первая точка в подпространстве описывает аккорды из трех нот (подпространство при этом выглядит как коническая плоскость) совпадает с мажорными трезвучиями, другая совпадает с альтерированными аккордами, в которых некоторые ноты на полтона выше, и так далее.

Музыкальные произведения также можно рассматривать как дороги через описываемое пространство. Но поскольку новая карта более полная, новые отношения теперь видятся яснее. Например, Тимочко утверждает, что его подход раскрывает тип отношений между аккордовой последовательностью у Дебюсси в «Прелюдии к послеполуденному отдыху фавна» и более ранней последовательностью в вагнеровской прелюдии к «Тристану и Изольде»; это сходство нельзя было обнаружить с помощью традиционных методов анализа двух последовательностей. Само собой, Дебюсси не имел представления о формальной математической связи его творения с произведением Вагнера, но Тимочко полагает, что подобные связи неизбежно возникают по мере того, как композиторы исследуют музыкальное пространство. Как альпинист обнаруживает, что лишь ограниченное число возможных маршрутов между двумя точками пригодно для освоения, музыканты эмпирическим путем открывают, что варианты передвижений ограничены исходными формами и структурами музыкальных возможностей.

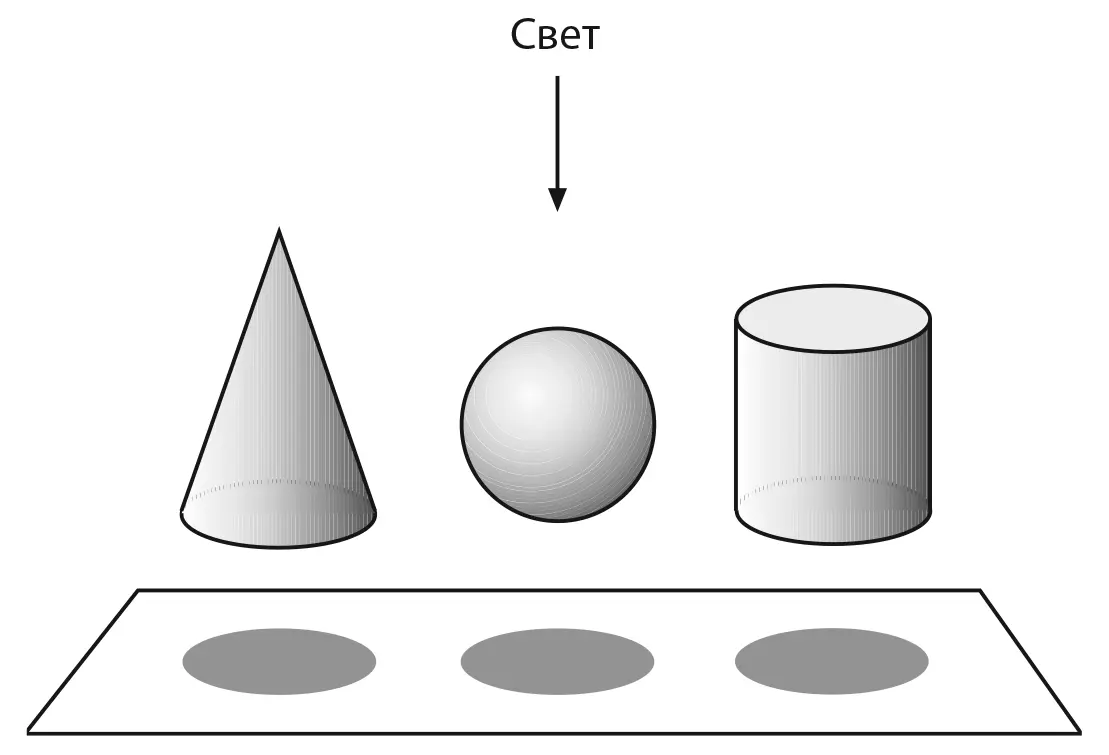
Рис. 6.30 Свойства симметрии могут выявлять соответствия между группами и последовательностями нот, упрощая музыкальное пространство. Точно так же трехмерные объекты можно «свернуть» в один класс путем проецирования на двухмерное пространство.