Ахун Андижани - Хамса. Пятерица

F = U – T ∙ S,

где U – внутренняя энергия системы;

T – абсолютная температура (в Кельвинах);

S – энтропия.

Из приведённой формулы видно, что при возрастании энтропии свободная энергия убывает. Заметим, что и внутренняя энергия, и свободная энергия, и температура (в Кельвинах) – неотрицательные величины.

Вышерассмотренный шарик в положении «в» фигуре 1 имеет свободную энергию, не равную нулю, но если не действуют другие внесистемные силы (то есть система

«потенциальная яма – шарик» замкнута), то в конце концов шарик очутится в положении «В», истратив свободную энергию на трение при движении к своему устойчивому положению «В», некоторое время совершая вокруг этого положения колебательные движения.

Уже творцы второго начала Клазиус и В. Томсон применили его ко всему миру в целом. Рассуждая, что если любая изолированная система стремится к возрастанию энтропии (а Вселенную можно считать замкнутой, изолированной системой), то в конечном итоге это означает неизбежную тепловую смерть Вселенной – её состояние, в которой никакие превращения энергии невозможны.

Эти рассуждения были подвергнуты острой и правомерной критике с различных позиций. Например, с космологической точки зрения, энтропия Вселенной всё время возрастает, но максимального значения нет, и она никогда не достигнет его (то есть состояния полного теплового равновесия для Вселенной не существует). С точки зрения статической физики, было показано, что энтропия выражает вероятность состояния системы, и возрастание энтропии означает переход системы от менее вероятных состояний к более вероятным. Но возрастание энтропии не носит абсолютного характера, а выражает лишь наиболее вероятное течение процессов. Для образований, включающих бесконечно большое число частиц (Вселенная, мир в целом), утрачивает смысл и само понятие наиболее вероятного состояния (в бесконечно большом образовании все состояния оказываются вероятными, а следовательно, равновесными).

Тем не менее для замкнутых, ограниченных систем второе начало термодинамики работает безукоризненно. Именно то обстоятельство, что нет примеров, противоречащих второму началу, приводит нас к уверенности в невозможности вечного двигателя. С точки зрения рассматриваемого подхода, второе начало термодинамики есть отражение стремления физических объектов к своему устойчивому состоянию.

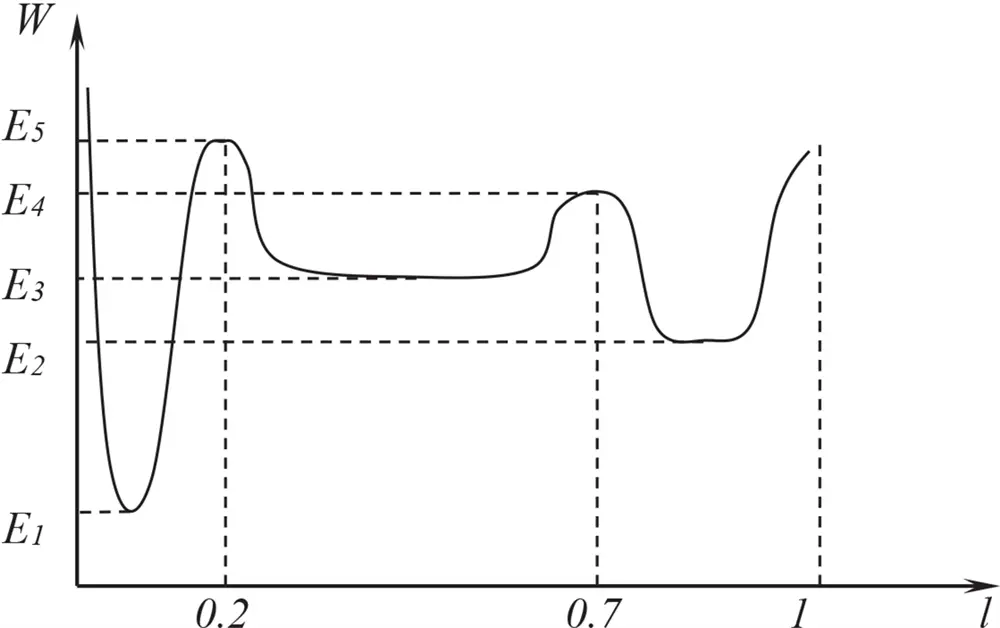
На примере исследованного выше шарика рассмотрим относительность эффективности всевозможных устойчивых положений в зависимости от величины воздействующих сил окружающей среды. Допустим, что потенциальное поле представляет поверхность, приведённую на фигуре 2 , с потенциальными ямами разного уровня (разной глубины).

Фиг. 2

Если энергия флуктуаций (возбуждений) не превышает разности энергий ( ∆E = E 4– E 3 ) для данного случая минимального потенциального барьера, то шарик будет находиться в довольно устойчивом стабильном состоянии, попав в любую из рассматриваемых потенциальных ям.

Если вероятность попадания в какую-либо яму зависит от линейных размеров ям, то наиболее вероятное устойчивое положение шарика, попавшего в эту систему, соответствует положению во второй яме. И хотя наиболее глубокой ямой, характеризуемой наибольшей устойчивостью, является первая яма, вероятность попадания в это наиболее устойчивое положение в рассматриваемом случае минимально. Вероятность попадания в третью яму занимает промежуточное положение.

Если энергия флуктуаций не превышает величину равности энергий второго по величине энергетического барьера ( ∆E 2= E 5– E 3 ), но может превышать величину ( ∆E min= E 4– E 3 ), то вероятность попадания шариков в разные потенциальные ямы перераспределится в пользу третьей ямы за счёт второй.

Если энергия флуктуаций превышает величину ∆E 2 , то вероятность попадания в первую яму повышается, но в определённом диапазоне энергий, опять же, за счёт только второй ямы и частично за счёт третьей ямы.

При очень большом количестве шариков необходимо учитывать и заполняемость потенциальных ям. При достаточно больших энергиях флуктуаций и достаточно продолжительном времени их воздействия в этом случае распределение шариков по ямам может приводить просто к закону сообщающихся сосудов. На фигуре 3 пунктирной линией проведён уровень заполненности ям шариками в этом случае.

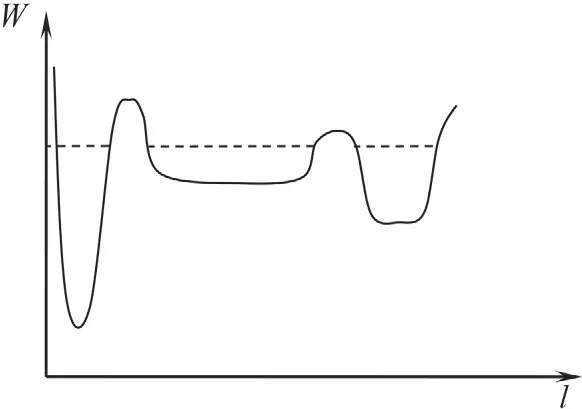
Фиг. 3

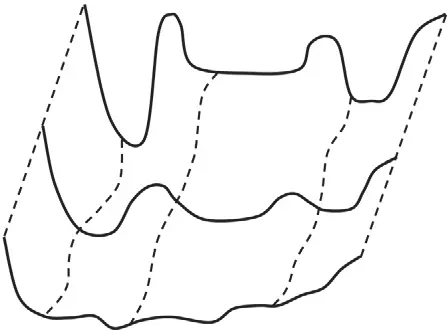
Фиг. 4

При изменении внешних условий, например, при изменении конфигурации поверхности водоразделов вниз по течению, как показано на фигуре, вероятности попадания в различные потенциальные ямы могут изменяться.

На практике указанная задача может иметь интерес при выборе места для гидроэлектростанции определённой мощности на одной из трёх горных рек и/или при выборе поля для влаголюбивых растений и т. д. В качестве рекомендаций может быть приведён соответствующий вывод о необходимости лесопосадок на каком-либо отроге, что повысит определённый энергетический барьер и будет способствовать снегозадержанию, например, во ворой или третьей ямах, с учётом действующих в этом районе ветров и т. д. Конкретные приложения указанной модели могут быть различными, но здесь этот пример приведён для того, чтобы показать, что:

1) в реальных условиях для одних и тех же объектов может быть несколько устойчивых состояний;

2) одни из них могут быть более устойчивыми, другие – менее устойчивыми;

3) в зависимости от возможного уровня воздействия внешней среды, вероятности реализации различных устойчивых состояний могут перераспределяться;

4) вероятности реализации различных устойчивых состояний могут меняться и с изменением внешних условий.

Для более чёткого представления о влиянии условий окружающей среды на переоценку эффективности различных устойчивых состояний вернёмся к уже частично исследованному примеру взаимодействия камня с Землёй. Выше пренебрежение силами трения привело к выводу о наличии трёх устойчивых состояний, реализуемых при различных значениях начальной скорости камня. Если принять в расчёт силы трения, то в промежуточном случае, когда начальная скорость камня меньше второй и больше первой космической, появляются качественно новые аспекты и выводы несколько изменятся. В промежуточном случае реализуется только относительно устойчивое состояние, которое в конце концов из-за действия сил трения о «звёздную пыль» окажется недостаточно устойчивым.