Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Внутри этого интервала, с длительностью равной характерному времени исторических изменений, процесс смоделированного роста будет качественно меняться. (Рост скорости роста будет сменяться ее убыванием.) Что возможно и в реальности, т. е. не противоречит историческим и демографическим данным.

В результате такой интерполяции получим кусочно-линейную функцию, аппроксимирующую гиперболу демографического роста. Причем отличие ее от гиперболы, т. е. отклонение линейного сплайна от гиперболы, будет гораздо меньшим, чем разброс демографических данных. Поэтому такая «кривая» может служить полноценной заменой гиперболе Форстера.

Иначе говоря, демографические данные соответствуют этому закону роста, полученному с помощью кусочно-линейной интерполяции, в той же степени, что и гипербола Форстера [79].

Конечно, все сказанное не является доказательством и позволяет создать лишь наглядный образ процесса построения необходимой зависимости. Однако доказать существование такой кривой роста или «сколь угодно» мало от нее отличающейся – не представляет особого труда.

И, наконец, сконструируем еще одну кривую следующим образом: возьмем иголку и прошьем нашу кусочно-линейную функцию по узлам – стежок за стежком. В результате получим то, что изображено на рис. 7. Всего будет 80 стежков.

Т. к. кривизна такой «стежковой» кривой N(t) при трех последовательных проколах меняет (возможно, неоднократно) свой знак, то скорость роста численности dN/dt оказывается немонотонной функцией. Действительно, в точках перегиба вторая производная N(t) меняет свой знак, а первая производная, соответственно, достигает максимума или минимума, т. е. рост (спад) скорости роста сменяется ее спадом (ростом).

Теперь «потянем» за нитку, которой прошили гиперболу. Дуги стежков можно «сколь угодно близко» подтянуть к отрезкам линейного сплайна, натягивая нитку. Следовательно, такая «стежковая» кривая может быть непрерывной со всеми своими производными и при этом «сколь угодно мало» отличаться от кусочно-линейной функции, т. е., имея немонотонно растущую производную dN/dt, соответствовать демографическим данным в той же степени, что и гипербола Форстера.

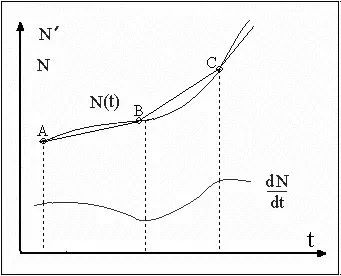
Рис. 1. Немонотонная зависимость скорости роста от времени при монотонном «гиперболическом» росте численности.

Итак, мы получили закон роста численности населения мира, отвечающий демографическим данным в той же мере, что и эмпирическая гипербола демографического роста, но при этом скорость роста этой численности за время от начала летоисчисления до второй половины ХХ века циклически, десятки раз меняет характер своей монотонности. И закон (1) пропорциональности скорости роста квадрату численности в этом случае, очевидно, уже не выполняется.

Отсюда с необходимостью следует, что все модели первого типа, основанные на (1) как на причинном законе, объяснить такой смоделированный рост не в состоянии.

Здесь может быть такое возражение: внутри интервала длительностью 40 лет скорость роста меняет характер своей монотонности, но при этом рост скорости роста превышает ее спад. А на интервалах, длительность которых значительно больше 40 лет, средняя скорость роста растет по закону квадратичной гиперболы. Следовательно, можно считать, что закон (1) в среднем все-таки выполняется.

Конечно, и для такого смоделированного нами роста среднюю скорость этого роста можно определять с помощью (1), и эта средняя скорость растет по закону (1) [80]. Но можно ли в таком случае вводить мгновенную скорость роста численности и составлять какие-то дифференциальные уравнения, ведь при конечно-разностном приближении производной нужно брать интервалы с длительностью, гораздо большей сорока лет.

Т. е. длительность эта должна составлять как минимум сотни лет, тогда как гипербола Форстера получена для исторического периода продолжительностью всего в 20 столетий.

Конечно, можно учесть циклическую динамику скорости роста внутри интервала длительностью 40 лет, связав ее, например, гипотетически с причинами, порождающими Кондратьевский цикл, но при этом с законом (1) все равно придется распрощаться.

Но что по настоящему важно, так это то, что для смоделированного здесь роста перестает работать та причинно-следственная связь, которая служит объяснением явлению гиперболического роста во всех моделях первого типа.

Т. е. рост численности может приводить и к спаду скорости роста, что делает неспособной, например, изобретательскую теорию Коротаева с ее формулой: больше людей – больше изобретателей – больше скорость роста – больше людей, объяснить смоделированный здесь рост.

Не работает в этом случае также и принцип демографического императива Капицы, согласно которому рост и развитие в эпоху гиперболического роста причинно определялись (т. е. растущая численность – причина роста и развития), прежде всего, растущей численностью населения мира.

Приведенная здесь модель роста численности с немонотонной, циклически меняющейся скоростью роста, всего лишь пример, показывающий, что зависимость скорости роста от численности населения Земли могла быть иной, отличной от той, что определяется законом (1).

Численность населения мира на протяжении тысячелетий (если исключить войны и эпидемии) всегда только росла. Но циклически могла меняться скорость ее роста и производные от нее.

В ХХ веке монотонность скорости роста нарушалась неоднократно, что связано прежде всего с мировыми войнами, однако к началу перехода рост вернулся на ту же самую гиперболу, которой следовал многие тысячи лет. Возможно, существует связь устойчивости роста с его немонотонностью.

Возможно, и в отсутствии катастроф динамика изменения скорости роста численности населения Земли во все времена носила циклический характер, что и обеспечивало устойчивый рост. Возможно, даже « назначение» экономических циклов и, в частности, Кондратьевского цикла как раз и заключается в том, чтобы обеспечивать такую устойчивость. Но это лишь предположение.

Закон квадратичного роста (1) Коротаев считает тем причинным, абстрактным законом, который полностью объясняет гиперболический рост. И даже претендует в определенном смысле на роль его первооткрывателя!

Рис. 1. Закон квадратичного роста скорости роста численности от численности (1) и гипербола Форстера – зависимость численности от времени (2).