Анатолий Молчанов - Население Земли как растущая иерархическая сеть

Это такое же ощущение, как и многие другие: от простых сигналов, идущих от органов чувств, до мистических откровений, природа которых остается загадочной. Ощущение, возникающее по причине возбуждения определенных зон в головном мозге, и оно может не только сопутствовать какому-то нашему поступку (а не возникать по его причине), но и вообще быть ложным, т. е. не соответствовать никакой реальности.

Например, это могут быть ложные, «имплантированные» представления. Так, в ряде экспериментов, описанных Вегнером, люди после определенной промывки мозгов признавали свою вину за нажатие «неправильной» клавиши компьютера, которую они в действительности не нажимали. Это ощущение может и полностью отсутствовать, в то время как человек активно производит какие-то действия. Вегнер, Карпентер и ряд других психологов заинтересовались необычным эффектом, происходящим во время спиритических сеансов:

«Когда мы совершаем желаемый поступок, нам свойственно трактовать это как проявление свободы воли. Однако иногда люди совершают поступок, а чувства реализованной свободы воли не испытывают.

Группа людей кладет руки на круглый стол, который может вращаться. Участники сеанса верят, что стол начнет вращаться по воле призванного ими духа. Нередко стол действительно приходит в движение, а все до единого участника группы готовы покляcться, что они не причастны к этому вращению.

Когда на стол кладут Библию, вращение ко всеобщему шоку останавливается. Проверить причастность духов к вращению стола можно по характеру отпечатков пальцев, оставляемых участниками спиритического сеанса на пыльной столешнице.

Одно дело, когда пальцы пассивно сопротивляются вращающемуся столу, и совсем другое, когда они активно раскручивают стол. Направление штрихов будет разным. Наблюдения показали, что люди, а не духи раскручивают стол. Но люди не ощущали свободы воли и потому испытывали иллюзию, что стол вращает кто-то другой» Daniel Wegner, «The Illusion of Conscious Will».

Далее, мы покажем, что даже если бы закон (1) и выполнялся в точности в течение всего социального периода развития человека, рост все равно не был бы гиперболическим, т. е. закон квадратичного роста в условиях реального демографического процесса не способен «вычертить» гиперболу Форстера. А причина такой неспособности заключается в отсутствии у уравнения (1) устойчивых решений.

Вопрос о причинах устойчивости гиперболического роста Коротаев вообще не рассматривает. А между тем устойчивость роста не менее парадоксальна, чем его глобальность. Человечество не раз проходило через бутылочное горлышко эволюции, когда численность популяции драматически снижалась до предельно низкого уровня.

Как показали исследования генетиков, в верхнем палеолите популяция находилась на грани вымирания. А во время неолитической революции, согласно ряду исследований, численность человечества сначала снизилась в десять раз, и лишь затем последовали фазы восстановления и взрывного роста.

Именно благодаря такой селекции расовые и этнические различия в геноме человека значительно меньше различий в геноме двух шимпанзе, взятых из разных популяций. И, возможно, благодаря такой селекции человеческая цивилизация вообще существует, по крайней мере, в том виде, в каком мы ее наблюдаем.

В средние века до тридцати процентов населения Европы вымерло от чумы, причем эпидемия длилась десятилетиями, а общие потери оцениваются в 25 млн или около 10 % населения мира. Этот отход от гиперболы очень хорошо виден на кривой роста численности мира по Бирабену.

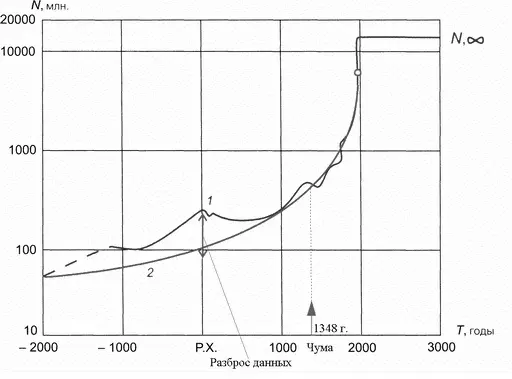
Рис. 1. Рост численности населения мира по Бирабену до 2000 года. Отход от гиперболы во время эпидемии чумы в Европе.

Общие потери в результате мировых войн ХХ века составили 150 млн или 7 % населения мира. При этом основные потери – это не военные потери на полях сражений. Их величина составляет 50 млн, остальные же 100 млн – это потери среди мирного населения, включая тех кто скончался от голода и болезней и тех, кто мог бы родиться, но не родился.

Парадокс заключается в том, что после каждого такого катастрофического спада численности возврат происходил всегда на одну и ту же гиперболу. Т. е. закон, управляющий ростом, обладает памятью. Но закон роста для простых моделей первого типа, построенных на законе квадратичного роста как на причинном законе, т. е. для моделей Коротаева и Капицы, не обладает не только памятью, но и устойчивостью.

Рис. 2. Закон квадратичного роста. Скорость роста численности населения мира пропорциональна квадрату численности.

Предположим, что закон роста (1) справедлив в точности, а не в тенденции, как считает Коротаев. Тогда после каждого спада численности в результате какой-то катастрофы или после каждого ее всплеска после внедрения какого-то полезного изобретения рост продолжается уже по новой гиперболе .

Дифференциальное уравнение (1) есть, по сути, рекуррентное соотношение, определяемое следующим образом: прирост численности за небольшой фиксированный промежуток времени Δ t равен некоторой константе (С -1 Δ t), умноженной на квадрат численности. Если задано начальное значение – процесс полностью определен. При разных начальных условиях получаются разные гиперболы. На языке аппарата дифференциальных уравнений – это задача Коши, и ее решение зависит от начального условия. После катастрофического спада численности рост идет уже по другой гиперболе, поскольку никаким механизмом устойчивости эта простейшая рекурсия, очевидно, не обладает.

Сразу же отметим, что под устойчивостью будем иметь в виду устойчивость по Ляпунову, но не просто устойчивость (шарик на столе), а асимптотическую или экспоненциальную устойчивость (шарик в лунке).

Следовательно, если бы рост происходил по Коротаеву, кривая роста состояла бы из отрезков идентичных с точностью до положения точки сингулярности гипербол роста, т. е. кусков гипербол от катастрофы – до катастрофы (или от скачка – до скачка).

Например, если бы в конце неолита численность людей, населяющих Ойкумену, уменьшилось в результате какой-то катастрофы всего на 10 %, то сингулярность эмпирической гиперболы демографического роста, сингулярность Дьяконова – Капицы, отодвинулась бы в будущее на 1000 лет. Если бы после эпидемии чумы в Европе эта численность росла по Коротаеву, то сингулярность Дьяконова – Капицы оказалась бы в XXII веке.