Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Сам Пифагор считал самым интересным число 36. Он полагал, что это идеальный возраст для мужчины (было ли у него какое-нибудь мнение об идеальном возрасте для женщины, я не знаю).

Математические свойства числа 36 впечатляли Пифагора, потому что:

36 = (1 + 2 + 3)² = 1³ + 2³ + 3³.

Когда я был моложе, я был согласен с Пифагором (и относительно вариантов выражения числа 36, и в том, что 36 лет – очень приятный возраст), но теперь я придерживаюсь более оптимистической точки зрения и считаю «идеальным возрастом» – как для мужчин, так и для женщин – 100 лет:

100 = (1 + 2 + 3 + 4)² = 1³ + 2³ + 3³ + 4³.

Те равенства, о которых мы только что говорили, далеко не случайны. Возможно, вы уже догадались, что квадрат суммы любого количества последовательных чисел равен сумме кубов всех этих чисел:

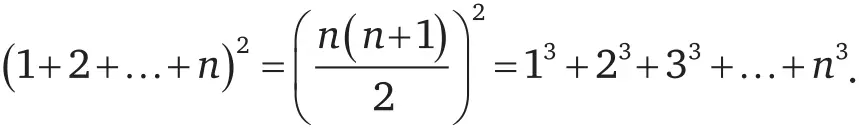
Мы обнаружили некоторые весьма интересные свойства некоторых чисел. Но наверняка существуют какие-то числа, в которых нет ничего по-настоящему уникального. Однако, если применить к числам парадокс «самого скучного человека на свете», то, может быть, число, не имеющее никаких особенных свойств, можно считать «интересным» именно этой особенностью.

Сриниваса Рамануджан был математическим гением. Он родился в 1887 г. в Ироду, в индийской провинции Мадрас, и уже в детстве проявил необычайные математические способности.

Однако там, где он жил, ему было не у кого учиться, и даже не было никого, кто смог бы посоветовать, чему учиться. Можно сказать, что Рамануджан был самоучкой. Хотя он не получил никакого формального образования, он добился беспрецедентных достижений в нескольких математических дисциплинах. Главной областью его работы была теория чисел, и, подобно Пифагору, Рамануджан поддерживал с числами близкие личные отношения.

В 1913 г. Рамануджан отправил несколько своих математических результатов (равенств, или тождеств) трем известным британским математикам, но лишь один из них, Годфри Гарольд Харди, сумел понять, насколько блестящим человеком был автор этих результатов. Хотя эти результаты во многом были подобны неотшлифованным алмазам, они все равно были прекрасны. Харди приложил все усилия, чтобы перевезти Рамануджана в Лондон, а затем, во время Первой мировой войны, – в Кембридж. Впоследствии Рамануджан стал первым индийцем, избранным членом кембриджского Тринити-колледжа.

Ниже представлены два из тех самых результатов (равенств), которые так поразили Харди. Когда я впервые увидел эти равенства, я был третьекурсником математического факультета, и они были настолько прекрасны, что я сразу же подумал о музыке. Они казались мне нотами прекрасной симфонии. Эти равенства кажутся очень сложными, и они действительно сложны, но вам необязательно понимать их. Вам даже необязательно рассматривать их как математические выражения. Просто посмотрите на великолепную красоту, заключенную в этих численных узорах.

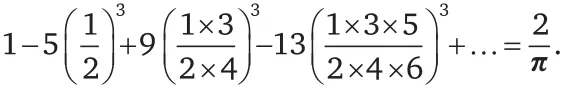
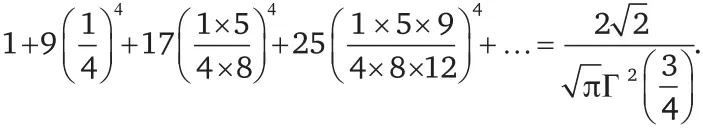
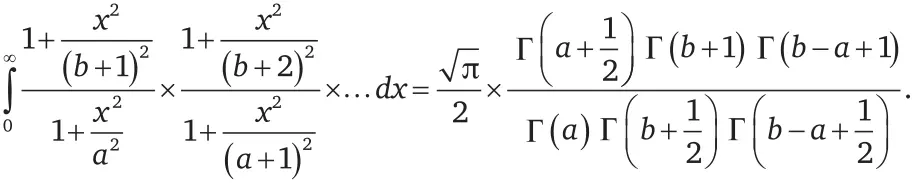
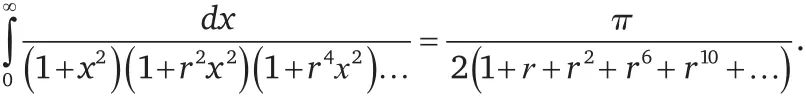
Какое великолепие!

Формула не имеет для меня смысла, если она не выражает мысли божества.

Хотя можно просто любоваться эстетическими аспектами математических формул Рамануджана, нам, возможно, захочется проявить некоторый педантизм и проверить, действительно ли его результаты верны.

Посмотрим на первое равенство.

У нас есть бесконечный ряд слагаемых, разделенных поочередно плюсами и минусами. Первое слагаемое – единица, но каждое следующее после него – произведение целого числа и дроби. Целое число каждый раз увеличивается на 4. Числитель дроби равен степени произведения нечетных чисел, а ее знаменатель – степени произведения четных чисел, причем количество множителей каждый раз увеличивается на единицу. Рамануджан утверждает, что чем больше в этой формуле сомножителей, тем ближе ее результат становится к двойке, деленной на π (отношение длины окружности к ее диаметру)! При бесконечном числе сомножителей результат будет в точности равен отношению двойки к π.

Откуда взялось это равенство? У Рамануджана были тысячи (!) таких формул (точнее, почти 3900). Вы, вероятно, не поверите, но те, что приведены выше, относятся к числу самых простых из них!

Чтобы быть до конца честным, я должен сказать, что некоторые из формул Рамануджана не были стопроцентно точными, но я твердо придерживаюсь того мнения, что из ошибок великого человека можно узнать гораздо больше, чем из истинных утверждений посредственности.

Харди и Рамануджан разительно отличались характерами. Харди был атеистом (и считал Бога своим злейшим врагом) и отличался исключительным педантизмом во всем, что касается математики: он хотел видеть доказательство каждой формулы. Рамануджан же был человеком во всех отношениях глубоко религиозным, а в отношении математики больше полагался на интуицию. Он не только видел в своих уравнениях и тождествах проявление божества, но и не любил рассказывать, как именно он к ним пришел, опасаясь, что его могут признать сумасшедшим. Это напоминает мне одну сцену из фильма «Амадей» Милоша Формана: Сальери читает ноты Gran Partita [12] Серенада № 10 си-бемоль мажор для духовых, KV361 (370A). Моцарта и приходит к уверенности, что ее продиктовал Моцарту сам Бог. Потом Сальери разглагольствует о том, почему Бог не выбрал его самого, чтобы продиктовать ему столь возвышенное сочинение. Видимо, некоторые считают, что гений может даваться только Богом.

Следующее равенство, на мой взгляд, – самая странная из формул Рамануджана:

1 + 2 + 3 + 4 + ··· = –1/12.

Что???

Она кажется совершенно неверной! Бесконечная сумма, которая стоит в левой части, должна быть равна бесконечности; из нее никак не может получиться отрицательного числа! Но, можете быть уверены, Рамануджан понимал, что он делает, и эта запись отнюдь не бессмысленна: он работал с очень важной дзета-функцией Римана – Эйлера (это функция комплексного переменного, рассмотрение которой выходит за рамки этой книги). Рамануджан писал в письме к Харди: «Согласно моей теории, сумма бесконечного числа членов ряда 1 + 2 + 3 + 4 + … = –1/12. Если я скажу Вам об этом, Вы сразу же ответите, что мне прямая дорога в сумасшедший дом».