Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

Все это может показаться сомнительным, но позвольте мне объяснить. Представьте себе, что доказательство для n – это костяшка домино. Если вы когда-нибудь выстраивали ряд костяшек домино, вы знаете, что их ставят так, что, когда некая определенная костяшка падает, она толкает соседнюю, та толкает следующую и так далее – пока не упадут все костяшки. В доказательстве по индукции мы точно так же выстраиваем свои «утверждения» в ряд: если мы доказали утверждение для любого элемента n , это «толкает» утверждение для элемента n + 1. Но, как и в случае костяшек домино, чтобы запустить цепную реакцию падения, нужно подтолкнуть первую костяшку – или, если использовать терминологию математической индукции, доказать базу индукции. Итак, мы совершаем индукционный переход – то есть предполагаем, что истинно следующее равенство:

1 + 3 + … + (2 n – 3) + (2 n – 1) = n ².

Теперь докажем, что оно справедливо и для n + 1, рассуждая следующим образом.

Левая часть равенства имеет вид:

1 + 3 + … + (2( n + 1) – 3) + (2( n + 1) – 1) = 1 + 3 + … + (2 n – 1) + (2 n + 1).

В правой же части должно быть ( n + 1)². Поскольку мы предполагаем, что наше равенство выполняется для n , мы можем утверждать, что:

1 + 3 + … + (2 n – 1) + (2 n + 1) = n ² + (2 n + 1) = ( n + 1)².

Этим завершается доказательство гипотезы индукции. Осталось только толкнуть первую костяшку. Для базы индукции, то есть при n = 1, утверждение, несомненно, справедливо, так как 1 = 1².

Теперь костяшки доказательства начинают падать одна за другой: утверждение для n = 2 вытекает из утверждения для n = 1, утверждение для n = 3 – из утверждения для n = 2 и так далее.

Однако Пифагор придумал способ получше этого. Тот же закон становится совершенно очевидным, если расположить камешки определенным образом.

Один шарик и три шарика легко расставить в форме квадрата размером 2 × 2 клетки:

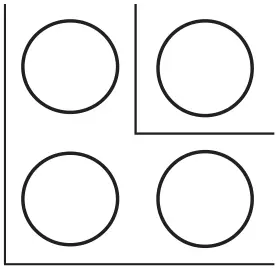
Один шарик, три шарика и еще пять шариков дают правильный квадрат размером 3 × 3:

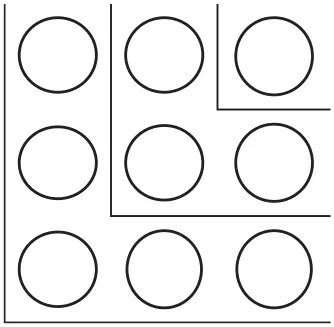
Если же добавить к ним следующее нечетное число, 7, точно так же получится квадрат размером 4 × 4 клетки:

Великий еврейский философ Барух Спиноза различал три вида знания:

1. Вера.

2. Исследование (экспериментирование).

3. Понимание.

Я объясню, о чем идет речь. Если вы сообщаете мне что-то – например что сумма последовательности нечетных чисел равна полному квадрату, – я могу поверить, что вы знаете, о чем говорите. Это первый уровень знания. Однако вполне может быть, что то, что вы мне рассказали, неверно.

Если я не поленюсь проверить эту информацию – то есть рассмотрю несколько примеров и смогу убедиться, что для них это правило выполняется, – я перейду на второй уровень знания. На нем утверждение несколько более достоверно, потому что я видел, что оно действительно справедливо в некоторых случаях, но считать его абсолютно истинным нельзя. Профессор Бено Арбель (1939–2013) показал мне однажды замечательный пример, в котором многократные проверки не позволяют убедиться в истинности утверждения, даже когда их число необычайно велико. Возьмем выражение 991 n ² + 1. Существует ли такое значение n , при котором это выражение дает полный квадрат? Можно подставить множество разных значений n , а потом перебрать кучу других значений n , и все время будет казаться, что это выражение никогда не дает полного квадрата. Но это не так, потому что при n = 12 055 735 790 331 359 447 442 238 767 получается именно полный квадрат! Даже если мы проживем миллиард лет и потратим все это время на подстановки и вычисления, вряд ли мы обнаружим это число.

А это подводит нас к третьему уровню: только если понять, почему нечто происходит, – например разложив камни квадратом, – можно исключить всякую возможность ошибки.

Скажи мне – и я забуду. Научи меня – и я запомню. Дай мне сделать – и я пойму.

Подход Пифагора нравится мне тем, что он дает знание третьего рода. Я понимаю, почему выражения верны, на более глубоком уровне. Я не могу проверить все бесконечное количество случаев применения формулы, но, если я получу глубокое понимание происходящего, я пойму, почему эта формула истинна.

Однажды мне попалась в библиотеке книга русского математика Якова Успенского (1883–1947) под названием «Теория уравнений» (Theory of Equations, 1948). Он работал в Стэнфордском университете под именем Джеймс Успенский. Успенский доказал множество разнообразных формул тем же путем, каким доказывал Пифагор, – то есть при помощи иллюстраций.

Начну с весьма простого примера.

Если сложить все числа от 1 до n , результат будет равен

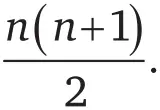
Следующий чертеж объясняет, почему эта формула действует для случая n = 4.

Сумма чисел от 1 до 4 равна половине площади прямоугольника; другими словами, ½ × 4 × 5 = 10.

Ну хорошо, для n = 4 все просто. А что происходит с более крупными числами?

Существует хитрый способ вычисления суммы последовательных чисел от 1 до, скажем, 100. Этот способ тесно связан с историей, главный герой которой – маленький мальчик. Разные страны и народы спорят о том, кто именно был этим мальчиком. Русские утверждают, что это был математик Николай Лобачевский, «Коперник геометрии», и было ему тогда семь лет. Евреи говорят, что это был Барух Спиноза, но возраст называют такой же. Немцы называют героем этого повествования выдающегося математика – на самом деле одного из величайших во всей истории математики – К. Ф. Гаусса (в честь которого, что неудивительно, названа колоколообразная кривая – гауссиана) в шестилетнем возрасте. Немало и таких родителей, которые утверждают, что это произошло с их собственным ребенком.

Поскольку мы только что познакомились на страницах этой книги со Спинозой, я выберу его.

Так вот, однажды маленький Барух сидел на уроке и очень, очень скучал. Но беда была не только в том, что ему было скучно, а еще и в том, что из-за этого он шалил и мешал учителю вести урок. Учитель решил дать мальчику какую-нибудь задачу, которая займет его на долгое время, и велел Баруху сложить все числа от 1 до 100. «Этого ему хватит по меньшей мере до конца урока», – решил учитель.