Хаим Шапира - Восемь этюдов о бесконечности. Математическое приключение

В 1949 г. Капрекар установил, что число 6174 можно считать пределом последовательности следующих операций. Возьмем любое четырехзначное число, не все цифры которого одинаковы. Переставим его цифры так, чтобы получить наименьшее и наибольшее из возможных чисел. Вычтем меньшее число из большего. Если их разность равна 6174, процесс завершен. Если нет, повторим те же действия. В конце концов всегда получается 6174.

Попробуем проделать это с номером года, в котором я начал писать эту книгу, – 2009. Наибольшее число, которое можно образовать из этих четырех цифр, – 9200, а наименьшее – 0029. Вычтем 29 из 9200 и получим 9171.

Повторим эту процедуру: 9711 – 1179 = 8532.

Продолжим: 8532 – 2358 = 6174. Наши поиски завершены: в конце пути нас с самого начала поджидало число 6174.

На математическом языке 6174 называется «неподвижной точкой», что означает следующее: если мы подставим в этот процесс само это число, мы снова вернемся к нему же. Проверим: 7641 – 1467 = 6174. Действительно, дальше дороги нет; путешествие подошло к концу.

А что, если немного схитрить? Получится ли этот же фокус с числом, в котором есть три одинаковые цифры? Скажем, с числом 1112? Давайте попробуем.

2111 – 1112 = 999

Поскольку мы работаем с четырехзначными числами, запишем результат в виде 0999.

9990 – 0999 = 8991

9981 – 1899 = 8082

8820 – 0288 = 8532

8532 – 2358 = 6174

Вот мы и на месте.

Если кому-нибудь из вас остро требуется трудотерапия, можете попробовать проделать это с какими-нибудь другими числами.

Теперь у нас появилась превосходная возможность поставить свой собственный маленький математический эксперимент. Что получится, если использовать не четырехзначные, а трехзначные числа?

Попробуем, например, взять число 169.

961 – 169 = 792

Кстати, 169 = 13², а 961 = 31². Но не будем отвлекаться.

972 – 279 = 693

963 – 369 = 594

954 – 459 = 495

Мы пришли к неподвижной точке (проверьте, что это так!). Неужели мы открыли постоянную Капрекара для трехзначных чисел? Именно это мы и сделали! Если вы увлекаетесь алгеброй, вам не составит особого труда доказать это утверждение.

Перейдем к двухзначным числам. С ними-то все должно быть совсем легко, правда?

Начнем с одного из моих любимых чисел – 17.

71 – 17 = 54, 54 – 45 = 9, 90 – 9 = 81, 81 – 18 = 63, 63 – 36 = 27, 72 – 27 = 45, 54 – 45 = … Минуточку! Здесь мы уже были! Что происходит? На самом деле мы пришли к точке периодичности. Для двухзначных чисел неподвижной точки не существует.

А что получается с пятизначными числами? А с шестизначными?

Капрекар обнаружил, что некоторые числа обладают одним необычным свойством: если возвести такое число в квадрат, то получившееся число можно разбить на две части, сумма которых будет равна исходному числу. Эта концепция станет яснее, если привести несколько примеров:

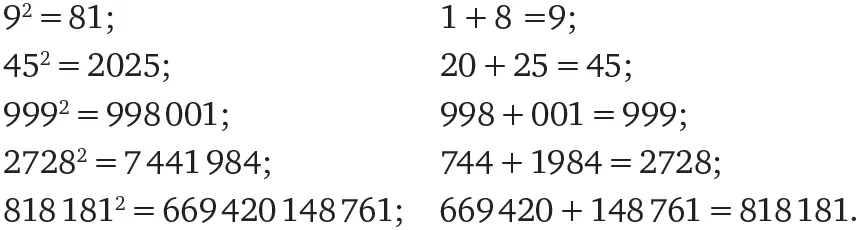
Числа 9, 45, 999, 818 181 – и многие другие – относятся к сообществу «чисел Капрекара». Вы можете запустить на своем компьютере простую программу, которая познакомит вас со многими другими представителями этого сообщества.

Докажите, что числа 9, 99, 999 и 9999 – это числа Капрекара.

Найдите следующее число в последовательности: 1, 2, 4, 8, 16, 23, 28, 38, 49…

Подумайте несколько минут. Если вы не сможете решить эту задачу, ответ можно найти в примечаниях в конце книги {13} 13 Ответ – 62. Каждое число последовательности равно сумме предыдущего числа и суммы цифр предыдущего числа. Например, после 16 идет 23, потому что 16 + (1 + 6) = 16 + 7 = 23. Следовательно, ответ задачи: 49 + 13 = 62. .

Интересная особенность этой задачи заключается в том, что ее обычно бывает трудно решить почтенным математикам, потому что они углубляются в поиски сложных идей. Легче всего эта задача дается умным детям.

Капрекар заметил, что некоторые числа можно получить сложением меньшего числа с суммой его цифр, а для других чисел это оказывается невозможным. Например, число 40 можно получить этим методом, взяв 29 (2 + 9 = 11, 29 + 11 = 40). Но число 20 таким образом получить невозможно, с какого бы числа мы ни начинали (проверьте, так ли это).

Капрекар сформулировал критерий, по которому можно определить, какие числа невозможно получить при помощи этого метода [15] В русской терминологии такие числа (например, число 20) называются самопорожденными , в отличие от порожденных чисел (например, числа 40; число 29 называется его генератором ). . Я не хочу лишать вас удовольствия самостоятельно воссоздать этот критерий. Дам лишь небольшой совет: найдите первое число, удовлетворяющее этому критерию, и попытайтесь вывести общее правило.

А теперь вернемся к нашему великому герою – Пифагору.

Представьте себе, что вы учитесь не в школе, а ходите на уроки на пляж. Здорово, правда? Именно так поступали пифагорейцы. Пифагор любил изображать числа шариками или камешками, выложенными на песке. По-разному располагая эти камешки, он придумал несколько математических формул и концепций.

Посмотрим на некоторые примеры.

Каждый, кто помнит хоть что-то из школьного курса, вероятно, может вспомнить и следующий закон: сумма n первых последовательных нечетных чисел, начиная с 1, всегда равна квадрату n .

Проиллюстрируем это утверждение:

1 + 3 = 4 = 2²;

1 + 3 + 5 = 9 = 3²;

1 + 3 + 5 + 7 = 16 = 4²

и так далее.

Те, кто продолжал углубленно изучать математику в старших классах, вероятно, знают, что этот закон можно доказать при помощи концепции, которая называется математической индукцией.

Математическая индукция – это совершенно поразительный инструмент для доказательства утверждений. Что особенно замечательно, он позволяет получить доказательство для бесконечного множества элементов исходя из доказательства для конечного их числа. Я приведу пример, объясняющий, как работает индукция. Предположим, мы хотим доказать, что следующее равенство справедливо для всех натуральных чисел:

1 + 3 + … + (2 n – 3) + (2 n – 1) = n ².

Доказательство состоит из двух частей. В первой части мы доказываем справедливость так называемого индукционного перехода , то есть несколько странного утверждения, которое гласит: «Если это равенство истинно для n , то оно истинно и для n + 1».

Во второй части нужно доказать так называемую базу индукции , то есть убедиться, что это равенство истинно для n = 1.

Вот и всё! Этим мы доказываем справедливость этого утверждения для всех натуральных чисел.