Бен Орлин - Время переменных. Математический анализ в безумном мире

Проще простого, да только, как я полагаю, все это не сработает.

Через столетие после Джевонса команда психологов во главе с Даниэлем Канеманом [53] Израильско-американский психолог, один из основоположников поведенческой экономики, в которой объединены экономика и когнитивистика для объяснения иррациональности отношения человека к риску в принятии решений и в управлении своим поведением. – Прим. пер. начала исследование непосредственного опыта людей при страдании: испытуемых заставляли опускать кисти рук в ледяную воду. (Психология – это социология для социопатов.) Одну руку погружали в воду температурой около 14° С на одну минуту. В другой раз вторую руку подвергали такому же испытанию, добавив дополнительные 30 секунд пребывания в воде, причем за это время температура постепенно повышалась до 15° С.

Позднее испытуемых спрашивали, какой опыт они повторили бы с большей готовностью.

По теории Джевонса никто не должен выбирать последний путь. В нем есть вся леденящая боль первого опыта плюс еще немного. Если только вы не арктический тюлень и не мазохист (или все вместе), дополнительное время пребывания в ледяной воде вам не понравится.

И тем не менее большинство испытуемых выбрали именно это. Оглядываясь назад на пройденные испытания, люди склонны не обращать внимания на то, как долго они длились. Вместо этого они сосредотачиваются на критических точках и окончании – на максимуме боли и на уровне боли в конце. Поскольку во втором опыте критическая точка была той же самой, а окончился он на несколько менее болезненной ноте, испытуемые вспоминали его более доброжелательно.

Эмоции в том виде, в каком они хранятся в человеческой памяти, не похожи на интеграл Джевонса. Перевешивают всегда последние из них. Вспоминаю одно высказывание Рэя Брэдбери: «Яркий фильм с посредственным финалом – это посредственный фильм. Напротив, средний фильм с великолепной концовкой – это отличный фильм». Что делает историю счастливой или грустной, циничной или дарящей надежду, трагической или комической? Это окончание, и больше ничего. Именно поэтому мы торопимся к постели умирающего и долго думаем о его последних словах. Именно поэтому последние минуты жизни могут перевесить все предшествующие восемь десятков лет.

Основа, на которой строится утилитаризм, – это субъективный опыт. Человеческие эмоции. Временами это основание кажется не слишком прочным и скорее напоминает поток раскаленной магмы. Это серьезный вызов мечте превратить нравственность в математику.

Но даже если и так, утилитаризм остается мощным и нужным голосом в моральной сфере. Конечно, мы можем спорить о том, что считать «величайшим добром» («Лучше быть недовольным Сократом, чем всем довольным дураком», – сказал экономист XIX в. Джон Стюарт Милль), или кто входит в число «величайших людей» («Большинство человеческих существ – сторонники видовой дискриминации», – предупреждал философ Питер Сингер), или как собрать миллиард субъективных знаний в единое множество (может быть, Лев Толстой сможет помочь?). И пусть мы отвергаем исчисление счастья по Джевонсу, но всякий раз, придумывая свои способы подсчитать то же самое – новые варианты, больше учитывающие сложную эмоциональную составляющую, – мы идем по его стопам. Явно или нет, последовательно или не очень, мы проживаем свои жизни, так или иначе исчисляя счастье.

Вы слышали о римлянах: упрямые, несговорчивые, начисто лишенные чувства юмора, да вдобавок это «наши-мраморные-обломки-будут-лежать-здесь-еще-тысячу-лет». В 212 г. до н. э. их армия подошла к побережью Сицилии, чтобы захватить непокорный маленький город Сиракузы. Историк Полибий отмечает, что они прибыли вооруженные до зубов, на 60 кораблях, «наполненных лучниками, пращниками и копьеметателями», захватив с собой четыре огромные осадные лестницы.

Но Сиракузы знали старую поговорку: «Попав в руки римлян, поступай, как римлянин». То есть сражайся, как с чертями в аду. Из маленьких и больших катапульт жители Сиракуз обрушили на римлян «град камней» и дождь железных дротиков. Затем из стен города появились огромные механические когти, хватавшие римские корабли и «бросавшие их на острые скалы или на дно моря». Историк Плутарх рассказывает: «Бо́льшая часть Архимедовых машин была скрыта за стенами, и римлянам казалось, что они борются с богами – столько бед обрушивалось на них неведомо откуда» [54] Здесь и далее цит. по: Плутарх. Сравнительные жизнеописания. В 2 т. – М.: Наука, 1994 / Пер. С. П. Маркиша. .

Но дело обстояло намного хуже. Они сражались с Архимедом.

В обойме величайших математиков всех времен и народов Архимед единодушно признается ученым «первого ряда». Галилей называл его «суперчеловеком». Лейбниц твердил, что этот грек изменил само представление о гениальности, выставив более поздних мыслителей скучными и обыденными по сравнению с ним. «В голове Архимеда было больше воображения, – писал Вольтер, – чем у Гомера». Впрочем, Архимед, разумеется, никогда не получал Филдсовскую медаль – самую почетную в математике, но в его защиту можно сказать, что лицо мыслителя изображено на этой медали.

Хотите получить представление о его уме? Возьмите куб и разрежьте его на три равные части.

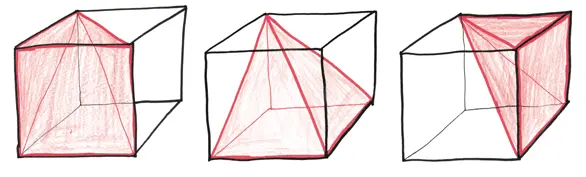
Три получившиеся фигуры – это идентичные пирамиды, каждая из которых имеет квадратное основание и острую вершину над одним из углов основания. Таким образом, каждая из них должна занимать 1/3 объема первоначального куба.

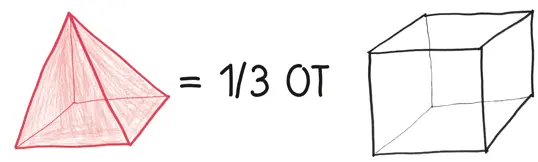
Пока все идет замечательно, но мы только начали.

Возьмите одну из этих пирамид и нарежьте ее на бесконечное количество чрезвычайно тонких ломтиков. Если я сделаю это правильно – а, принимая во внимание мою неуклюжесть в обращении с обычными кухонными ножами, вы, возможно, захотите лишний раз проверить мою работу с этим бесконечным концептуальным ножом, – каждое поперечное сечение должно быть идеальным квадратом.