Бен Орлин - Время переменных. Математический анализ в безумном мире
- Название:Время переменных. Математический анализ в безумном мире
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2021
- Город:Москва
- ISBN:9785001394525
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Бен Орлин - Время переменных. Математический анализ в безумном мире краткое содержание
Тема движения времени находит отражение и в названиях частей книги – «Мгновения» и «Вечности», и в ее персонажах – от Шерлока Холмса до Марка Твена и Дэвида Фостера Уоллеса. C присущими ему юмором и изобретательностью Орлин выявляет связи между матанализом, искусством, литературой и любимой собакой по имени Элвис.
Автор нашумевшей «Математики с дурацкими рисунками» и в этой книге ставит своей целью не просто увлечь читателя любимым предметом, но сделать нас более мудрыми и вдумчивыми.
Время переменных. Математический анализ в безумном мире - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
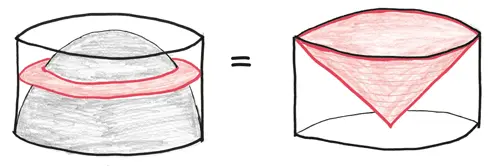
Как мы уже установили, конус заполняет 1/3 цилиндра. Таким образом, пустое пространство – то есть то, что было полусферой – заполняет 2/3.
Вывод: сфера заполняет 2/3 цилиндра.
Над этими чертежами на сицилийском песке Архимед мечтал об интегралах за тысячелетие до их изобретения. Площади и объемы, бесконечное количество ломтиков, перестановки, которые решают проблему непрерывности и кривизны, – все это химические ингредиенты, «первичный бульон», из которого позднее развились интегралы. Почему же тогда миру так долго пришлось ждать рождения математического анализа?
В тот день римляне взяли город. В течение нескольких часов Сиракузы были сожжены, а солдаты впали в состояние неистовства, грабя и убивая. «Множество жестокостей было совершено сгоряча и из жажды наживы», – писал историк Ливий. Тем не менее римский военачальник Марцелл настаивал на том, чтобы сохранить жизнь великому геометру, «находя в том, чтобы спасти Архимеда, столько же славы, сколько и в разрушении Сиракуз» (по словам другого историка).
Архимед даже не заметил падения города. Что значит какой-то грабеж и разрушения по сравнению с всепоглощающей красотой фигуры на песке?
Историки расходятся во мнении по поводу того, что сказал Архимед, когда к нему приблизился римский солдат. Возможно, он взмолился: «Пожалуйста, не стирайте мои круги!» Может быть, он разбушевался: «Не трогай моих чертежей, парень!» Весьма вероятно, что он прикрыл рисунки ладонями, как будто идеи значили намного больше, чем его собственная жизнь: «Лучше ударьте меня по голове, только не стирайте линии!» В любом случае все источники сходятся в одном: солдат убил Архимеда. Кровь заполнила прочерченные в песке дорожки, оставленные его пальцами. Марцелл настоял на подобающем погребении и осыпал родственников ученого подарками и милостями. Но виновник «бесчисленных бед» был мертв.
Сегодня величайшим наследием Архимеда считаются не катапульты и когти, а геометрия. Его понятные аргументы, его восприятие бесконечности, то, как близко он подошел к математическому анализу. Мог ли один легкий дополнительный толчок привести к нему? Мог ли матанализ возникнуть на Земле на тысячу лет раньше, чем это произошло в реальности?
Обдумайте высказывание математика Альфреда Норта Уайтхеда:
Гибель Архимеда от рук римского солдата – символ перемен первой величины в масштабе всего мира. Греки с их любовью к абстрактной науке уступили лидерство в европейском мире практичным римлянам.
В практичности в целом ничего плохого нет. Или все-таки есть. Премьер-министр Великобритании XIX в. Бенджамин Дизраэли определял практичного человека как «практикующего ошибки своих предков». Согласно Уайтхеду, именно это и делали римляне. Нигде в победившей стране вы не смогли бы найти искру воображения, которая была у побежденных.
Все их усовершенствования состояли в мелких технических деталях. Они не были мечтателями в достаточной степени… Ни один римлянин не поплатился жизнью за то, что был поглощен созерцанием математического чертежа.
Столетия спустя, когда жители Сиракуз забыли о наследии Архимеда, писатель Цицерон предпринял попытки отыскать его могилу. Он нашел ее, «скрытую кустами ежевики и терновника»: «маленькую колонну, едва видневшуюся над зарослями». Цицерон узнал могилу по тому, что было вырезано на ней, как и просил Архимед: сфера и цилиндр. Могила давно исчезла, но она запечатлелась в нашем коллективном воображении, которое может пережить пыль, кровь и все каменные строения, созданные руками римлян.
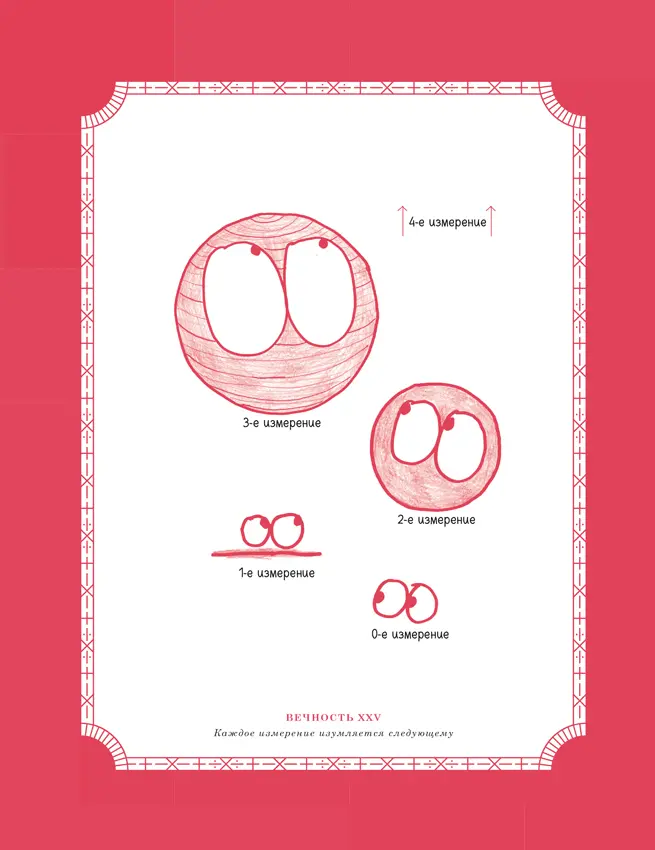
XXV
Из невидимых сфер
Мир «Флатландии» – романа о многих измерениях [56] «Флатла́ндия» (англ. “Flatland: A Romance of Many Dimensions”) – роман Эдвина Э. Эбботта. – Прим. пер.
– понятен из его названия. Место действия этого произведения, написанного в 1884 г., является абсолютно плоским: оно более плоское, чем блин, чем лист бумаги, чем женские характеры в фильмах Майкла Бэя. Это мир двух измерений, где имеются длина и ширина, но нет высоты. Тем не менее его обитатели – треугольники, квадраты, пятиугольники и так далее – не ощущают отсутствие одного измерения. На самом деле они, как канзасцы в Канзасе и техасцы в Техасе, не могут представить существование вне своего мира.
Пока в один прекрасный день не появляется очень странный визитер.
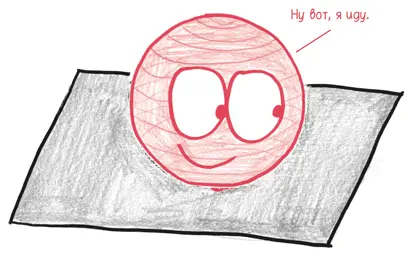
Вначале сфера выглядит всего лишь как точка, появившаяся из ниоткуда. Затем, по мере ее прохождения через Флатландию, рассказчик (по имени Квадрат) видит окружность, постепенно растущую в размерах.
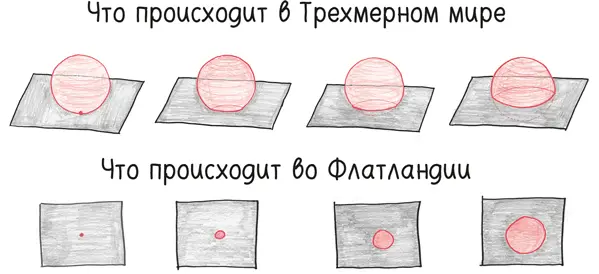
В самом деле необычайно! Представьте себе, что бы вы чувствовали, если бы какой-то парень прошел через дверь и в этот момент увеличился в росте от 1,2 м до 1,8 м. (Возможно, вы бы ощутили себя, как я каждый раз, когда веду уроки у девятиклассников.) Квадрат задался вопросом, что же за чертовщина здесь происходит, но получил только зашифрованные ответы наподобие этого:
Вы называете меня Окружностью, но в действительности я не Окружность, а бесчисленное множество Окружностей различных размеров, от Точки до Окружности, достигающей тринадцати дюймов в диаметре, как бы сложенных вместе. Пересекаясь с вашей Плоскостью, я образую в сечении Фигуру, которую вы с полным основанием называете Окружностью. Ибо даже Сфера (так называют меня обитатели страны, в которой я живу), если у нее возникает необходимость предстать перед обитателями Флатландии, вынуждена принимать форму Окружности [57] Эбботт Э., Бюргер Д. Флатландия. Сферландия / Пер. Ю. А. Данилова. – СПб.: Амфора, 2015.
.
С помощью этих странных разглагольствований сфера находит способ рассказать о своей природе. Сфера – это стопка бесконечного множества дисков, отличающихся радиусом и чрезвычайно тонких. Понять сферу означает совместить – суммировать – все эти маленькие круги в единое целое.
Сфера – это интеграл окружностей.
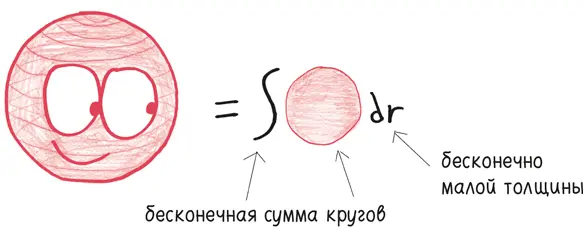
Если вы посещали курс математического анализа на первом году обучения, то ранее уже встречались с этим понятием. Это завершающая тема, где лихо закручивается идея трехмерности.
Читать дальшеИнтервал:
Закладка:









![Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]](/books/1150749/stiven-strogac-beskonechnaya-sila-kak-matematicheski.webp)
