Бен Орлин - Время переменных. Математический анализ в безумном мире

Самый нижний квадрат представляет собой основание куба. Самый верхний выходит таким крошечным, что является одной-единственной точкой. Между этими двумя крайними случаями есть множество других квадратов промежуточного размера.

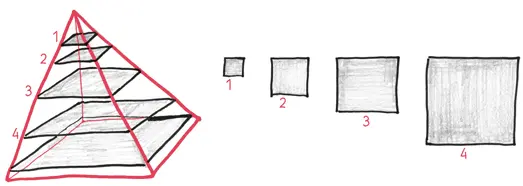
Теперь перейдем к дальнейшим действиям. Представьте себе эти квадраты как стопку бесконечного количества карт, каждая из которых толщиной с волос. Если перекладывать их с места на место, то объем не изменится, так что поехали! В данный момент у всех наших квадратов есть общий угол. Но почему бы не переместить их так, чтобы у них был общий центр? Это превратит нашу асимметричную пирамиду странного вида в классическую, в египетском стиле.

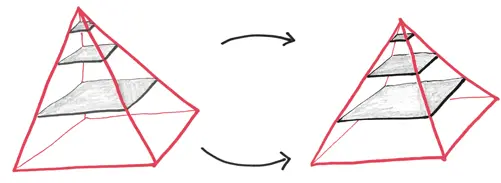
Самое замечательное – это то, что объем не изменяется. Он так и остается 1/3 от объема куба.

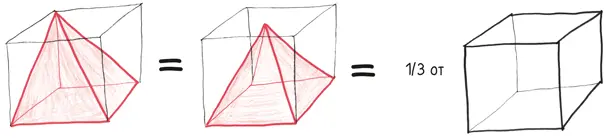
Теперь мы подошли к настолько гениальному и удобному шагу, что, когда математик Бонавентура Кавальери переоткрыл его в начале XIX в., его назвали «принципом Кавальери». На самом деле этот принцип придумал Антифон (V в. до н. э.), развил Евдокс (IV в. до н. э. – в действительности он впервые привел аргумент, о котором я говорю сейчас) и усовершенствовал Архимед (III в. до н. э. – вскоре мы доберемся до его уникального дополнения). Я собираюсь назвать его в честь охватившей ряды римлян паники «принципом бесчисленных бед».

Идея проста. Если вы имеете дело с трехмерными фигурами, то объем не меняется, когда вы заменяете одни поперечные сечения другими той же площади. Например, мы можем поменять наши квадраты на прямоугольники. Объем полученной теперь продолговатой пирамиды по-прежнему составляет 1/3 призмы, ранее известной как куб.

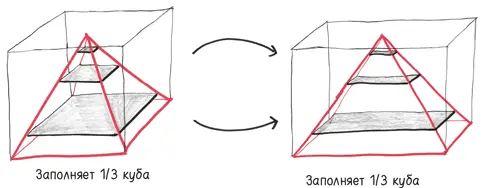
Или – эндшпиль великого гроссмейстера – мы можем превратить наши квадраты в круги . Неважно, что в действительности это делается с помощью карандаша и бумаги, называется квадратурой круга и по-настоящему невозможно. На практике – это для гимнастов, мы же с вами скользим по облакам чистой геометрии. Поэтому просто представьте, как каждый квадрат медленно превращается в круг, а площадь его не меняется.

Наша пирамида становится конусом. Наш куб становится цилиндром. И, таким образом, конус составляет 1/3 цилиндра, который содержит его.

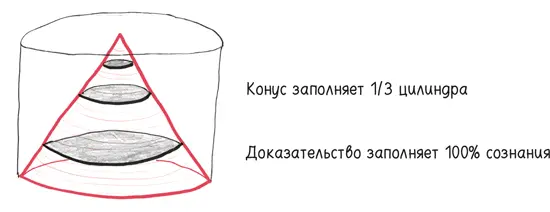
Довольно круто, правда? Во II в. Плутарх писал:

…во всей геометрии не найти более трудных и сложных задач, объясненных посредством более простых и прозрачных основных положений… Собственными силами вряд ли кто найдет предлагаемое Архимедом доказательство, но стоит углубиться в него – и появляется уверенность, что ты и сам мог бы его открыть: таким легким и быстрым путем ведет к цели Архимед.

Тем не менее эти экскурсы в геометрию не описывают «военного гения». Читатель должен поинтересоваться: откуда взялись военные машины, сразившие римлян?

«Сам Архимед считал сооружение машин занятием, не заслуживающим ни трудов, ни внимания, – отмечал Плутарх, – большинство их появилось на свет как бы попутно, в виде забав геометрии». Как бы странно это ни звучало, такое часто происходит в истории математики. Бесцельная игра фантазии каким-то образом ведет к технологическому прорыву.

Хотя римляне не особенно оценили чисто математические достижения, они явно отдали должное смертельным когтям, крушившим их суда. Распознав в себе грабителей из древнего приквела к «Один дома», генерал Марцелл и его армия отступили.

В один прекрасный день несколько месяцев спустя Архимед рисовал фигуры на песке. Мне нравится представлять, что он вспоминал свое любимое доказательство – теорему, которую он велел друзьям и родным написать на его могиле.

Она начинается со сферы.

Мы заключаем ее в цилиндр, идеально подогнанный, как упаковка – к теннисному мячу.

Вопрос Архимеда заключался в следующем: какую часть цилиндра заполняет сфера?

(В действительности вопрос был более элементарным: насколько велика сфера? Но любое описание размера требует ссылки на что-то, что нам уже известно: к примеру, мой рост – это приблизительно 5 2/3 [55] Примерно 174 см. – Прим. ред. тех давно существующих единиц, которые называются футами. И тут-то в дело как раз и вступает цилиндр.)

Для начала разрежем всю фигуру пополам. Вместо теннисного мяча в контейнере мы получим полусферу в хоккейной шайбе.

Теперь, вместо того чтобы беспокоиться об объеме внутри полусферы, мы можем сосредоточиться на объеме вне ее. В духе «бесчисленных бед» мы можем считать эту область пачкой обручей или шайб, каждая из которых является окружностью с круглой дырой в середине.

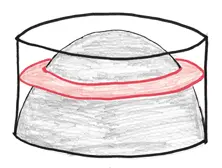
Внизу этой стопки находится чрезвычайно тонкая шайба. Ее дыра занимает весь круг, оставляя только напоминающее струну кольцо. Наверху тем временем пребывает очень толстая шайба. Это почти целый круг с отверстием размером с булавочный прокол. Между ними находится целое семейство шайб.

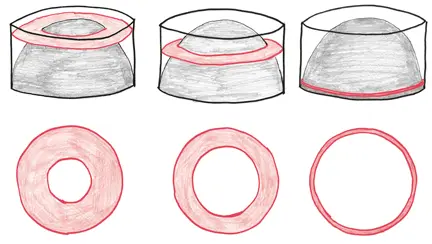
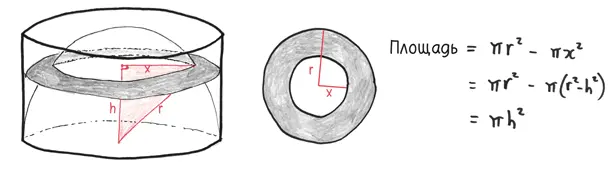
Каковы площади этих фигур? После интерлюдии с хитрой алгеброй мы приходим к выводу, что площадь каждой равна π h 2, где h – расстояние от поверхности.

Это означает, что, применяя Принцип бесчисленных бед, каждую из них можно заменить кругом радиусом h .

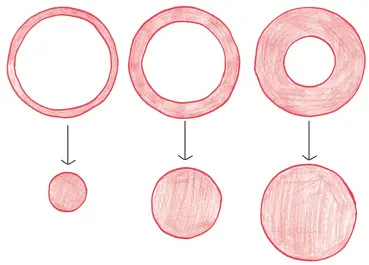
Видите! У нас получился не странный кратер в форме полусферы, а простой конус, перевернутый острием вниз.