Бен Орлин - Время переменных. Математический анализ в безумном мире

(Предупреждение: если вы чувствительны к укачиванию и плохим каламбурам, обратите внимание на слово «закручивается».)

Для начала возьмите плоскую двухмерную область. Затем раскрутите ее вокруг оси, как жесткий флажок вокруг палки. Пространство, через которое она проходит, оформится в виде трехмерного объекта, называющегося «тело вращения».

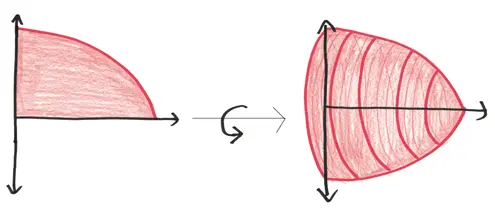
Это вращение, как на гончарном круге, превращает двухмерные области в трехмерные объекты, Флатландию – в Трехмерие. Если вы хотите узнать объем созданного нами тела, подход будет очень простым: проанализируйте его как стопку бесконечного количества плоских дисков и объедините их.

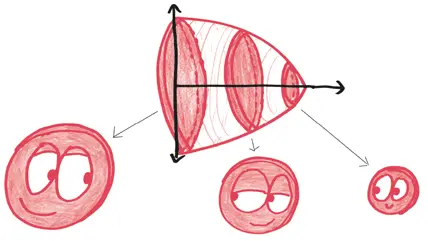
Чтобы высчитать объем сферического «злоумышленника», вначале мы должны выбрать подходящую двухмерную область. Какая форма при вращении вокруг своей оси, как цыпленок на вертеле, создаст сферу с диаметром 13 см?

Подключите свой внутренний 3D-принтер, и, думаю, вы обнаружите, что этот фокус проделывает полукруг.

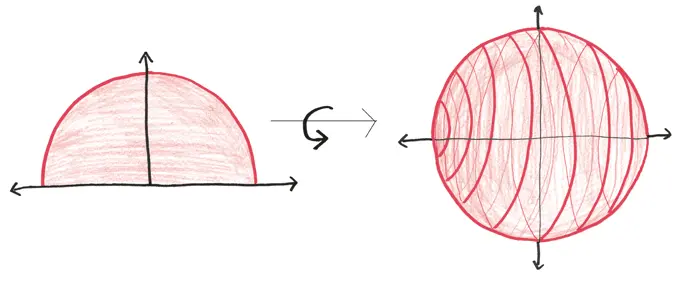
Забавный факт про полуокружности: они полны радиусов. Забавный факт про радиусы: каждый из них является гипотенузой прямоугольного треугольника. Это означает, что координаты каждой точки полуокружности подчиняются теореме Пифагора.

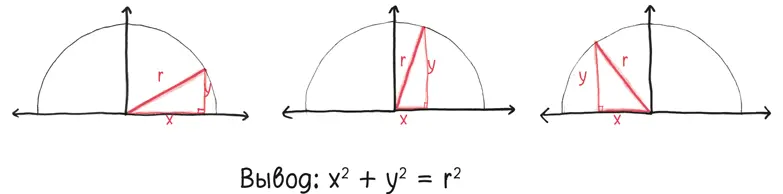
После небольших алгебраических манипуляций, которые я, как и любой рачительный хозяин, замел под ковер, чтобы спрятать из виду, мы получаем соответствующий интеграл. Это будет бесконечное количество бесконечно тонких дисков. Они начинаются с нулевого радиуса, возрастают до радиуса 6,5, а затем снова уменьшаются до нуля. Совсем как сфера, проходящая через Флатландию.

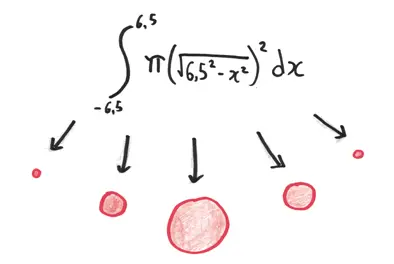
Я снова скрою от вас алгебраические детали и дам вам непосредственно конечный результат. Объем таинственной сферы равен 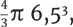или приблизительно 1150 кубических единиц.

В двух идущих друг за другом главах мы рассчитывали объем сферы. Возможно, вы заметили общие моменты. Оба метода начинают с того, что задача делится на две части, оба предполагают бесконечное рассечение, в обоих есть забавные картинки. И тем не менее они оставляют совершенно разное послевкусие, не так ли? Я лично предпочитаю доказательство Архимеда. Оно быстрое. Оно здравое. Детали в нем хорошо подогнаны друг к другу. Это работа мастера, это искусность и даже искусство.

Что же касается подхода с «телом вращения» – я не могу сказать, что он тешит душу. После многообещающего эстетического начала (вращение! бесконечные слои!) он заканчивается несколькими строчками грубой алгебры. Это словно прогулка пешком, которая каким-то образом ведет с живописной вершины холма в терминал аэропорта. Элегантная загадка, таким образом, сводится к упражнению.

И в этом-то все дело!

Мы все не можем быть Архимедами. На самом деле статистика доказывает, что никто из нас им не является. Если мы будем полагаться на космические озарения, чтобы решить стоящие перед нами задачи, нам придется ждать тысячелетия. Чтобы что-нибудь сделать, нам нужно превратить мистику в механику, текучее в статичное, невыразимое в нечто, что можно описать.

Тела вращения полностью выражают эту мысль. Любой из нас может спокойно пройти по пути, который раньше мог проделать только Архимед. В этом вся суть математического анализа: дать системный подход к решению задач, пугающих своей сложностью. Сделать каждого из нас Архимедом на автопилоте. Огромное семейство фигур – от кубов и конусов до пирамид и фигурок Микки-Мауса – можно рассечь и изучить с помощью тел вращения.

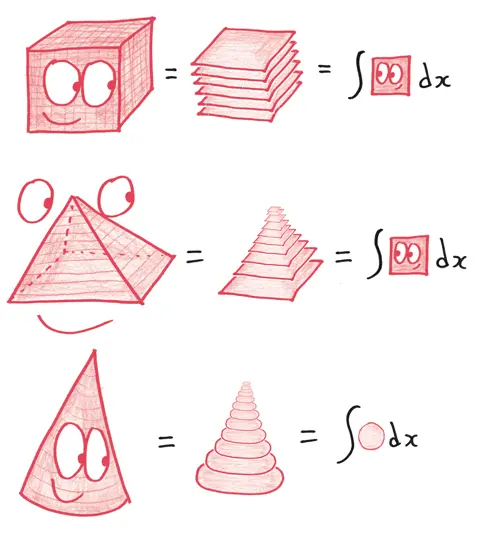
Как бы все это могло выглядеть для нашего героя из Флатландии, неустрашимого, но несколько обескураженного Квадрата? Вспомните, в начале истории он не мог видеть третье измерение. И даже не мог представить его. Чтобы понять его рассказ о том, что представляет собой жизнь во Флатландии,

положите на какой-нибудь стол в своем Пространстве монету достоинством в один пенни и, наклонившись над столом, посмотрите на него сверху. Монета покажется вам кругом.

Приняв затем вертикальное положение, начните медленно приседать таким образом, чтобы луч вашего зрения постепенно приближался к поверхности стола (а вы сами все более и более приближались бы к состоянию обитателей Флатландии). Вы увидите, что монета перестанет казаться вам кругом и примет овальную форму. Когда же, наконец, луч вашего зрения совместится с поверхностью стола (а вы как бы станете флатландцем), то монета вообще перестанет быть овалом и покажется вам, как вы сможете убедиться, отрезком прямой.

Как трехмерные создания мы можем видеть в двух измерениях, наше поле зрения словно холст художника или экран кинотеатра. По тому же самому принципу двумерные обитатели Флатландии могут видеть в 1D. Их поле зрения – это линия горизонта, выше и ниже которой ничего нет.

Так как же тогда вы объясните третье измерение этому бедолаге? В романе все попытки Сферы кончаются ничем.

Я: Не могли бы вы, ваша милость, указать или объяснить мне, в каком направлении простирается неизвестное мне третье измерение?

Незнакомец: Я прибыл к вам из третьего измерения. Оно простирается вверх и вниз.

Я: Ваша светлость, по-видимому, хотела сказать к северу и к югу?

Незнакомец: Ничего подобного! Говоря о третьем измерении, я имел в виду направление, в котором вы не можете взглянуть, потому что у вас нет глаз сбоку.

Я: Прошу прощения, ваша светлость, но достаточно даже беглого взгляда, чтобы ваша милость могла убедиться: там, где сходятся две мои стороны, у меня расположено великолепное око.

Незнакомец: Не спорю, но для того, чтобы вы могли заглянуть в Пространство, вам необходимо иметь глаз, расположенный не на периметре, а на боку: на том месте, которое вы скорее всего назвали бы своей внутренностью. Мы в Трехмерии называем ее нашей стороной.

Я: Иметь глаз в своей внутренности! Глаз в собственном желудке! Ваша милость шутит [58] Там же. – С. 99–100. .