Бен Орлин - Время переменных. Математический анализ в безумном мире

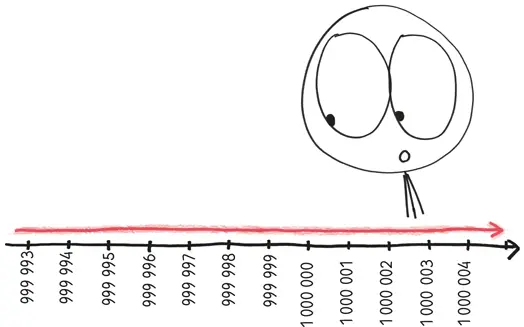
К тому времени, когда х добирается до миллиарда – то есть если вы читаете эту книгу в Лос-Анджелесе, то он находится где-то около Москвы, – y составляет По моим расчетам, это половина ширины атома гелия.

Тем не менее кривая движется, так и не пересекая ось, к неисчислимому горизонту, который мы называем «бесконечность».

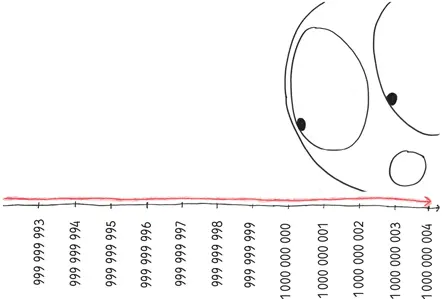
Теперь мы должны закрутить эту кривую вокруг оси х , чтобы, рисуя тело вращения, получить трехмерную фигуру. Эта имеющая веретенообразную форму красота – собрание неисчислимого множества дисков, каждый из которых бесконечно тонок, – и есть труба Гавриила.

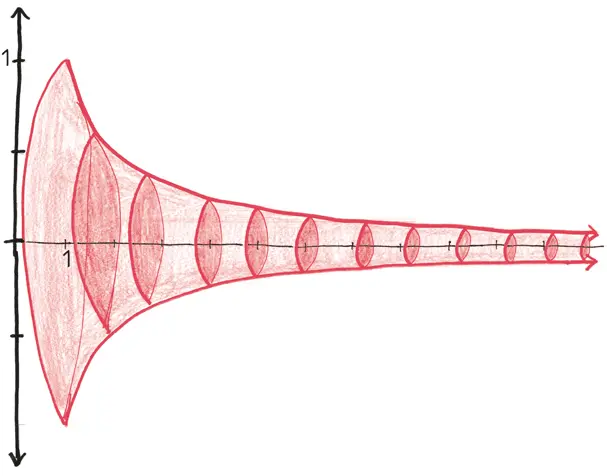
Как и любой трехмерный объект, «труба» позволяет провести два вида измерений. Во-первых, мы можем измерить ее объем – то есть какое количество кубических единиц воды требуется, чтобы ее наполнить. Во-вторых, мы можем измерить площадь ее поверхности – иначе говоря, сколько рулонов оберточной бумаги потребуется, чтобы ее завернуть.

Итак, сперва объем. В физической реальности бесконечный объект не может иметь конечный объем; нам нужна труба, которая становится тоньше атома, так что даже самые лучшие моторные навыки не позволят ее удержать. Но математика располагает другим видом реальности, где такое проявление ловкости – дело обычное. Поэтому, используя стандартные методы, мы получаем интеграл 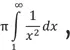который равен π. Таким образом, объем трубы Гавриила составляет 3,14 кубических единицы с поправкой в ту или иную сторону.

Теперь площадь поверхности. Интеграл получается несколько более ужасающим: Но он только немного больше, чем куда менее пугающий интеграл 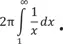Оказывается, все это равно… ну, какого-то определенного числа нет. Он неограниченно растет. И поскольку площадь поверхности немного больше этого интеграла, то мы можем заключить, что площадь трубы Гавриила равна ∞.

Вот мы и оказались на пороге противоречия. У трубы Гавриила есть конечный объем, то есть вы вольны заполнить ее краской, вы это можете. Тем не менее у нее нет конечной площади поверхности: при всем желании у вас не получится ее покрасить.

Но… если вы наполните ее краской, не будет ли это значить, что каждая точка поверхности окрашена?

Как и то и другое одновременно может быть правильным?

Первым, кто исследовал эту парадоксальную фигуру, был итальянский математик XVII в. Эванджелиста Торричелли. Вместе со своими приятелями Галилеем и Кавальери он прокладывал «королевскую дорогу через математические чащи», используя новомодную на тот момент математику бесконечно малых величин. «Очевидно, – писал Кавальери, – что плоские фигуры должны пониматься как куски, сплетенные из параллельных линий, а объемные тела – как книги, состоящие из параллельных страниц».

Эти ученые были поглощены бесконечными суммами, бесконечно тонкими элементами и странными объектами, такими как труба Гавриила, которая также известна как «труба Торричелли».

Это был математический анализ, выбирающийся из своей колыбели.

В то время орден иезуитов создал достойную восхищения систему университетов по всей Европе. Это были не просто хорошие учебные заведения, это были католические школы. «Для нас, – сказал один из лидеров ордена, – уроки и научные занятия – это нечто вроде крюка, на который мы будем ловить души». В этой учебной программе математика играла главную роль. «Без сомнений, – заявил один из иезуитов по имени Клавий [61] Христофор Клавий – германский математик и астроном, член ордена иезуитов. Прославился своим участием в комиссии по календарной реформе, созданной папой Григорием XIII. – Прим. пер. , – математические дисциплины занимают среди всех остальных первое место».

Но не просто любая математика: она должна была быть евклидовой. Евклидова геометрия развилась с помощью четкой логики от самоочевидных предположений до нерушимых заключений без единого сбоя или парадокса. «Теоремы Евклида, – говорил Клавий, – сохраняют… свою истинную чистоту и неоспоримую несомненность». Иезуиты видели у Евклида модель самого общества, где власть папы является неопровержимой аксиомой.

Что касается работы Торричелли, иезуиты не относились к числу его фанатов. Историк Амир Александер в своей книге «Бесконечно малые: как опасная математическая теория сформировала мир» (Infinitesimal: How a Dangerous Mathematical Theory Shaped the World) объясняет: «Тогда как евклидова геометрия являлась строгой, чистой и неопровержимо верной, новые методы были наполнены парадоксами и противоречиями и с равной вероятностью вели как к ошибке, так и к истине». Иезуиты считали трубу Гавриила анархистской пропагандой, угрозой порядку. «У них была тоталитарная мечта о неопровержимой истине и цели, которая не оставляла места сомнениям и спорам», – говорит Александер. Как подытожил Игнатий [62] По всей видимости, имеется в виду Игнатий де Лойола, основатель ордена иезуитов. – Прим. пер. , еще один иезуит того времени: «То, что кажется нам белым, черно, если так говорит Церковь».

Таким образом, папа запретил бесконечно малые. Торричелли стал математическим преступником, а труба Гавриила – интеллектуальной контрабандой.

Ирония в том, что этот парадокс не так уж трудно разрешить. Как труба Гавриила может иметь внутреннюю часть, которую можно наполнить краской, и внешнюю часть, которую нельзя покрасить? Все это зависит от того, как мы думаем об этом процессе.