Бен Орлин - Время переменных. Математический анализ в безумном мире

Как объясняет математик Роберт Гетнер, парадокс строится на предположении о том, что «площадь поверхности» соответствует тому, что нужно покрасить. Но окрашивание не является двумерным. «Если мы планируем покрасить комнату, – пишет он, – мы не будем просить 1000 квадратных метров краски». Как и бумага, окраска трехмерна. У слоя краски есть толщина, пусть и очень маленькая.

Поэтому первый подход: позволить толщине слоя краски постепенно исчезать, становиться все тоньше и тоньше вместе с трубой Гавриила. Пользуясь этим предположением, возможно покрыть поверхность конечным количеством краски. Парадокс разрешен.

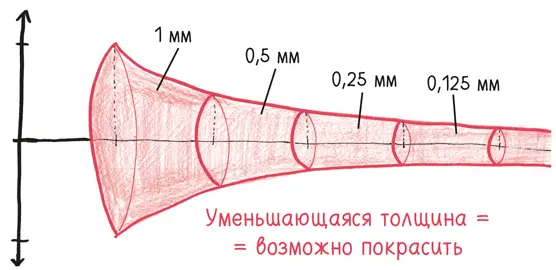
Или, если хотите, вы можете выбрать другой подход. Предположим, что для слоя краски нужна некоторая минимальная толщина. (Это больше похоже на окрашивание в физическом мире; например, краска не может лечь слоем толщиной в 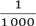от размера атома.) Таким образом, двигаясь вниз по оси, труба истончается до субатомных масштабов, но со слоем краски этого не происходит. В конце концов он станет в миллиарды раз толще окрашиваемого предмета. Это возвращает нас к нашему первоначальному выводу, что трубу невозможно покрасить. Только теперь еще и невозможно наполнить ее краской, потому что в определенный момент она становится тоньше, чем самая маленькая частица краски.

Если следовать этому предположению, то трубу невозможно ни окрасить, ни наполнить краской. И снова парадокс разрешен.

Я не могу однозначно сказать, совершили ли иезуиты начала XVII в. религиозную ошибку. Но я полагаю, что с математикой они ошиблись. Парадокс – это не то, чего следует бояться, и не то, что нужно истреблять. Это повод поразмыслить, приглашение к изучению.

Парадоксы произрастают не только в отдающих плесенью закоулках теологии и математики, но также, по словам профессора в области предпринимательства Марианны Льюис, и в корпоративной обстановке. Элементы, которые «кажутся вполне логичным, если рассматривать их отдельно» – краткосрочные цели, долгосрочный прогноз, стратегический приоритет, – становятся «иррациональными, противоречивыми и даже абсурдными, если совместить их». Это не обязательно плохо. «Парадоксы дают пищу способности к творчеству, – пишет Льюис. – Понимание парадокса может содержать ключ к тому, как справиться со стратегическими затруднениями и даже стать лучше, столкнувшись с ними». Парадокс – это песчинка, которая помогает создать жемчужину теории.

Дуглас Хофштадтер, автор книги «Гедель, Эшер, Бах: эта бесконечная гирлянда» [63] Хофштадтер Д. Гедель, Эшер. Бах: эта бесконечная гирлянда. Метафорическая фуга о разуме и машинах в духе Льюиса Кэрролла. – Самара: Бахрах-М, 2001. , пошел дальше. «В стремлении уничтожить парадоксы любой ценой, – пишет он, – слишком много внимания уделяют плоской последовательности и логичности и слишком мало тому причудливому и замысловатому, что придает вкус жизни и математике». Парадоксы прекрасны сами по себе, а работы Эшера хороши и без краски. Или, в данном случае, с бесконечным окрашиванием.

Мое первое прикосновение к Неберущемуся Интегралу состоялось весной, когда я учился в десятом классе.

Группа выпускников собралась в коридоре. Они были вооружены ручками и покрывали плакат закорючками, подписями и выдернутыми из контекста цитатами высказываний нашего учителя физики мистера Риахи. Это был обширный коллаж, полный шуток, которых я не понимал, шуток, которые я понимал наполовину, и шуток, которые мне очень хотелось понять.

Среди всего этого хаоса я заметил необычную мешанину символов:

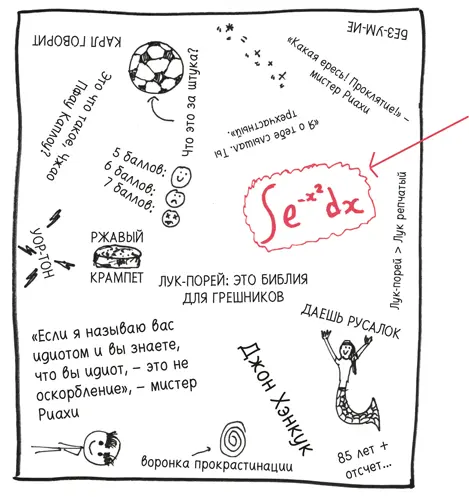
Я указал на нее:

– Что это?

– Это интеграл e в степени – х в квадрате, – объяснил Дэвид, не прояснив ничего.

– Так в чем же шутка? – спросил я.

– ШУТКА В ТОМ, ЧТО ОН НЕБЕРУЩИЙСЯ, – ответила Эбби, которая всегда разговаривала, словно писала большими буквами.

– А-а-а-а-а… его проверяли? Никто не смог его решить?

Они захихикали.

– АХ, НЕДОУЧКА БЕН, ТРЕТИЙ ИЗ ТРЕХ, – обратилась ко мне Эбби (так оно и было: Бен Копанс и Бен Миллер стояли передо мной в алфавитном списке). – КАКОЙ ТЫ НЕВИННЫЙ И ТРОГАТЕЛЬНЫЙ!

– Как бы то ни было, если под проверкой ты имеешь в виду «когда-либо во Вселенной», – задумчиво сказал Барт, – то да. Его проверяли. И никто не смог его решить.

– То есть это как… делить на ноль? – спросил я.

– Скорее как делать из круга квадрат, – ответил Дэвид.

– ЭТО КАК ДОЖДЬ В ДЕНЬ ТВОЕЙ СВАДЬБЫ! – уточнила Эбби. – КАК ДЕСЯТЬ ТЫСЯЧ ЛОЖЕК, КОГДА ВСЕ, ЧТО ТЕБЕ НУЖНО, – ЭТО НОЖ!

Эбби была права. Если вернуться в детство математического анализа, Иоганн Бернулли писал об угрозе неберущихся интегралов. «Иногда мы не в состоянии сказать с полной уверенностью, можем ли найти интеграл заданной величины». В XIX в. математик Жозеф Лиувилль сказал об этом с определенностью: некоторые интегралы взять нельзя. Например, 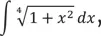или ∫ ln (ln x ) d x , или У этих интегралов нет чистых решений, точнее говоря, они «неразрешимы в элементарных функциях». Соберите все синусы, все косинусы, все логарифмы и кубические корни, какие вам захочется, но ни одна из стандартных алгебраических «отмычек» никогда не подойдет к формуле. Это замок без ключа, загадка без ответа, жесткий стейк в мире 10 000 ложек.

Я смотрел на символы. Большая загогулина не значила для меня ничего, пока еще нет. «Мы начнем матан через девять месяцев, – заметил ранее мой друг Роз, – и ты знаешь, что это означает: кто-то залетел от моего графического калькулятора». Шутку Роза я понял, но шутка выпускников ускользнула от моего ума.

Перенесемся на восемь лет вперед.

Моя первая работа в качестве преподавателя заставила меня задуматься о торговле подержанными автомобилями на окраине китайского квартала Окленда. Однажды на третий год преподавания я показал своим ученикам продвинутого курса математического анализа неберущийся интеграл: ∫ e −x2 d x . В витиеватых и напыщенных выражениях я разъяснил его нерешаемость.