Бен Орлин - Время переменных. Математический анализ в безумном мире

– Спойлер! – выкрикнула Адриана.

Несколько студентов покачали головами.

Но Бетсайда задала мне провокационный вопрос:

– Так у него нет области под кривой?

Ага, хорошая задачка! Думаю, никто не удивился, что я был небрежен и понятия не имел, как ответить на этот вопрос. Выяснилось, что у функции e −x2 есть чрезвычайно красивый график.

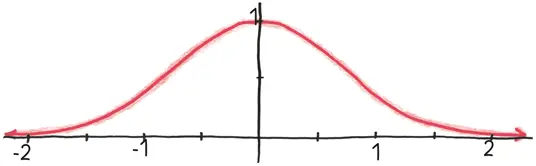
Если вы возьмете конкретную ограниченную область – скажем, от 0 до 1, или от 0,9 до 1,3, или от –1,5 до 0,5, то в самом деле найдете ответ.

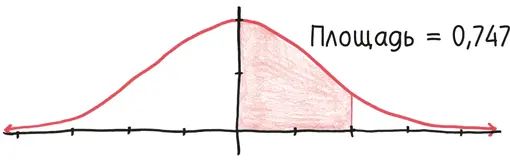
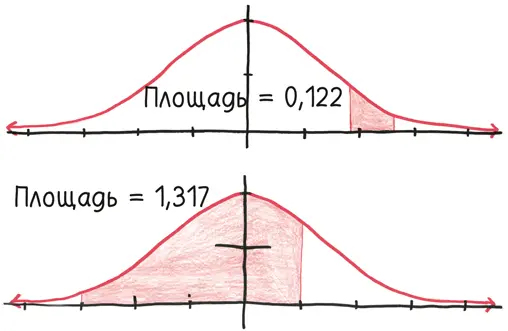
Тогда почему интеграл «неберущийся»? Потому что нет хорошей формулы для определения этой площади. Наша волшебная палочка – фундаментальная теорема математического анализа, которая вычисляет интегралы, беря антипроизводные, – здесь оказывается просто бесполезным прутиком. Машите ею хоть сотню лет: никакого магического ответа так и не появится.

– Мой графический калькулятор может это сделать, – сказал Ю Ханг. – То есть, если судить по вашим словам, он умнее всех математиков в мире.

– Ну… – я закашлялся. – Он определенно быстрее аппроксимирует интегралы через суммы Римана.

Самое лучшее, что мы можем сделать с такими функциями, – это аппроксимация. Мой тон выдавал мои предрассудки. Аппроксимация – это не настоящее решение. Она приблизительная. Второразрядная. Не считается.

– А вы уверены? – подзуживал Ю Ханг. – Этот калькулятор, кажется, умнее меня.

Когда урок закончился, я выскользнул из класса через заднюю дверь, которая в стиле Нарнии вела в кабинет статистики. Ее я преподавал первый год и все время спотыкался. Все мои инстинкты были чисто математическими, все доказательства и абстракции для статистики не подходили. Я чувствовал себя так, как будто перепутал виды спорта, словно учу детей сбивать подпрыгивающим теннисным мячиком кегли.

– Средний рост взрослого мужчины в США составляет 178 см, – начал я, – а стандартное отклонение – 9 см. Как много мужчин по нашим ожиданиям могут при этом иметь рост, по крайней мере, 2,14 м?

Как и очень многое в статистике, эта задача основывается на пологом уклоне кривой нормального распределения, также известной как колоколообразная кривая [64] Она же – кривая Гаусса. – Прим. пер. . Ее широко распространенная форма описывает ошибки в измерениях, диффузные частицы, показатели IQ, количество осадков, результаты большого количества подбрасываний монеты, а также, с некоторыми оговорками, рост человека. Итак, начинаем.

Шаг 1: 2,14 м – это 214 см.

Шаг 2: Это на 36 см больше среднего значения.

Шаг 3: Это четыре стандартных отклонения от среднего роста.

Шаг 4: Мы обращаемся к таблице в конце учебника и узнаем, что четыре стандартных отклонения соответствуют процентилю… Хм, в действительности таблица обрывается на 3,5 стандартных отклонениях. Упс!

Шаг 5: Извинившись, я вытаскиваю ноутбук и запускаю Excel, который может провести нас за край таблицы. Наш ответ – 0,999968. Другими словами, люди ростом 2,14 м встречаются в США с 99,9968 процентиля – приблизительно 1 на 30 000 человек.

Мы анализировали этот результат – иначе говоря, спорили об относительных преимуществах Шакила О'Нила [65] Шакил Рашоун О’Нил – американский баскетболист, комментатор, баскетбольный телеэксперт, рэпер, а также актер. Имеет рост 216 см. – Прим. пер. по сравнению с Яо Мином [66] Яо Мин – китайский баскетболист, спортивный комментатор, президент Китайской баскетбольной ассоциации. Имеет рост 229 см. – Прим. пер. , – когда меня вдруг осенило, что без всякого плана или предварительного намерения я провел два следующих друг за другом и очень разных урока по одной и той же теме.

Видите ли, кривая нормального распределения, которую мы используем, выглядит так:

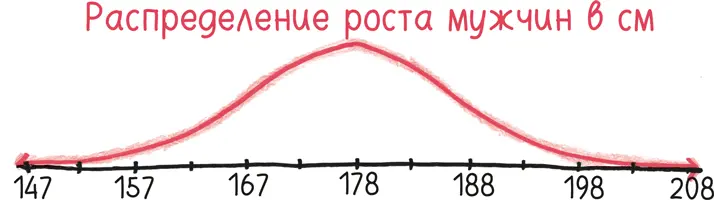
Это просто сглаженная версия графика функции: она сдвинута и приплюснута, но в душе остается той же самой функцией. Что означает: у нее нет интеграла. И тем не менее мы тут сидим и ее интегрируем. Каждый день. Постоянно.

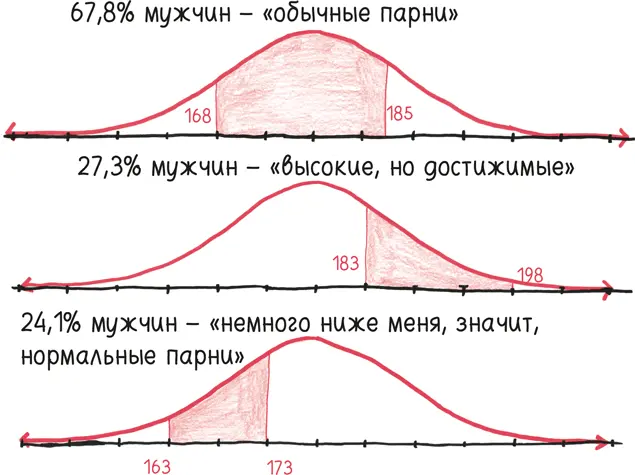
Не обращая никакого внимания на невозможность, вся статистика основывается на интегрировании того, что не может быть проинтегрировано. Каждой части населения (например, тем, чей рост находится в промежутке между 178 см и 188 см) соответствует область под кривой.

Природу не волнуют формульные антипроизводные. Таблицы в учебниках, заложенные в Excel формулы, графический калькулятор в рюкзаке Ю Ханга – все эти инструменты позволяют делать хорошие численные приближения. По большей части, это все, что вам нужно. Как подытожил Альберт Эйнштейн, «наши математические затруднения Бога не беспокоят. Он интегрирует эмпирически».

Я стоял у белой доски с маркером в руке. За молнией прозрения, как всегда, последовал медленный, раскатистый гром сожаления. Я хотел распахнуть дверь, которая отделяла кабинет математического анализа от кабинета статистики. Я хотел объяснить, каким дураком я был, покаяться в своем математическом шовинизме. «Абстрактные формулы, – хотел прокричать я, – не обязательно лучше конкретной аппроксимации! Бог интегрирует эмпирически, и эта правда делает нас свободными!»

Что удержало меня, кроме того, что этим я поставлю под вопрос свое психическое здоровье или (что примерно то же самое) прерву урок химии мистера Флеминга, это мысль об ухмылке Ю Ханга. «Я же вам говорил! – съязвил бы он. – Калькуляторы умнее математиков!» Не могу сказать за всех представителей моей профессии, но в моем случае я знал, что он был прав.

И снова переместимся во времени, теперь уже в сегодняшний день.

Я сижу в моем любимом кафе, потягиваю кофе сильной обжарки и занимаюсь «сбором информации» для книги, которую вы держите в руках (то есть отлыниваю от ее написания), и тут натыкаюсь на интеграл, названный в честь Карла Гаусса, как и многие другие вещи, которых он не открывал:

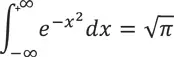
Кажется, из неберущегося интеграла есть исключение. Если заданная область включает в себя всю цифровую прямую от самого дальнего конца слева до самого дальнего справа, от одного неизмеримого горизонта до его недостижимого зеркального отражения, тогда ответ найти возможно.